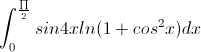Giải phương trình: 9|3x – 1| = 38x-2

Câu hỏi
Nhận biếtGiải phương trình: 9|3x – 1| = 38x-2
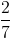
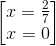

Đáp án đúng: B
Lời giải của Luyện Tập 365
PT <=> 32|3x - 1| = 38x-2 <=> 2|3x – 1| = 8x -2
Cách 1:
+ Xét TH1: 3x -1 ≥ 0 <=> x ≥ 
PT <=> 2(3x – 1) = 8x – 2 <=> 2x = 0 <=> x = 0 (loại)
+ Xét TH2: 3x – 1 < 0 <=> x < 
PT <=> -2(3x – 1) = 8x -2 <=> 14x = 4 <=> x= 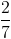 (thỏa mãn)
(thỏa mãn)
Cách 2:
PT <=> 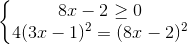
<=> 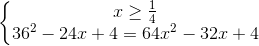 <=>
<=> 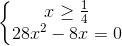
<=> 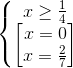 <=> x =
<=> x = 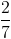
PT <=> 32|3x - 1| = 38x-2 <=> 2|3x – 1| = 8x -2
Cách 1:
+ Xét TH1: 3x -1 ≥ 0 <=> x ≥ 
PT <=> 2(3x – 1) = 8x – 2 <=> 2x = 0 <=> x = 0 (loại)
+ Xét TH2: 3x – 1 < 0 <=> x < 
PT <=> -2(3x – 1) = 8x -2 <=> 14x = 4 <=> x= 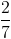 (thỏa mãn)
(thỏa mãn)
Cách 2:
PT <=> 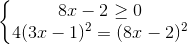
<=> 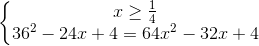 <=>
<=> 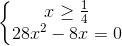
<=> 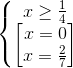 <=> x =
<=> x = 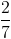
Câu hỏi liên quan
-

Trong mặt phẳng (P) cho tam giác đều ABC cạnh bằng a√6. Gọi M là trung điểm của AC và B' là điểm đối xứng với B qua M. Dựng điểm S sao cho SB' =3a và vuông góc với mặt phẳng (ABC). Gọi H là hình chiếu của M lên SB. Tính thể tích khối chóp H.ABC và góc giữa hai mặt phẳng (SAB) và (SBC).
-

Giải phương trình sin2x.(tan x - 1) = 3 sin x.(cos x + sin x) - 3.
-

Tính tích phân I=
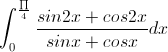
-

Tính tích phân I =
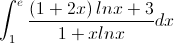
-

Tìm số phức z thỏa mãn
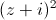 +
+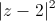 =2
=2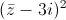 .
. -

Giải hệ phương trình
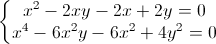 (x, y
(x, y R)
R) -

Giải phương trình:
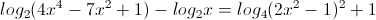
-

Giải phương trình
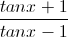 =
=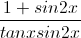
-

Trong không gian với hệ trục tọa độ Oxyz, viết phương trình đường thẳng ∆ nằm trong mặt phẳng (P): x+y-z+1=0, cắt các đường thẳng d:
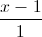 =
=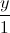 =
=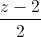 , d':
, d':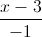 =
=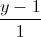 =
=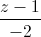 và tạo với đường thẳng d một góc
và tạo với đường thẳng d một góc 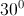 .
. -

Tính tích phân I=