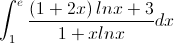Giải phương trình:
√3sin(3x -  ) + 2sin( 8x -
) + 2sin( 8x -  ) = 2sin(2x +
) = 2sin(2x +  ) + 3cos ( 3x -
) + 3cos ( 3x - 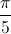 ) .
) .

Câu hỏi
Nhận biếtGiải phương trình:
√3sin(3x - 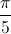 ) + 2sin( 8x -
) + 2sin( 8x - 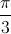 ) = 2sin(2x +
) = 2sin(2x + 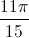 ) + 3cos ( 3x -
) + 3cos ( 3x - 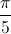 ) .
) .
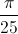 +
+ 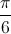 +
+ 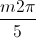 , x = -
, x = - 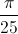 -
- 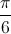 +
+ 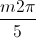 ; m∈ Z, x = -
; m∈ Z, x = -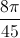 +
+ 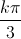 ; k ∈ Z.
; k ∈ Z. 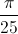 +
+ 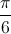 +
+ 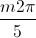 , x =
, x = 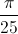 -
- 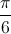 +
+ 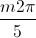 ; m∈ Z, x =
; m∈ Z, x = 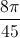 +
+ 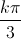 ; k ∈ Z.
; k ∈ Z. 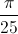 +
+ 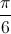 +
+ 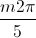 , x = -
, x = - 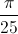 -
- 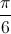 +
+ 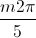 ; m∈ Z, x =
; m∈ Z, x = 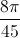 +
+ 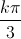 ; k ∈ Z.
; k ∈ Z. 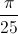 +
+ 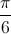 +
+ 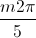 , x = -
, x = - 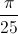 -
- 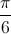 +
+ 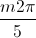 ; m∈ Z, x =
; m∈ Z, x = 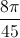 +
+ 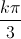 ; k ∈ Z.
; k ∈ Z. Đáp án đúng: D
Lời giải của Luyện Tập 365
Phương trình đã cho tương đương với √3sin(3x -  ) + 2sin(8x -
) + 2sin(8x - 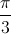 ) = 2sin(2x +
) = 2sin(2x + 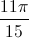 ) + 3cos(3x -
) + 3cos(3x -  )
)
⇔ 2sin(2x + 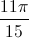 ) – 2sin(8x -
) – 2sin(8x - 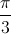 ) = √3sin(3x -
) = √3sin(3x -  ) – 3cos(3x -
) – 3cos(3x -  )
)
= √3( sin ( 3x -  ) – tan
) – tan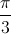 cos( 3x -
cos( 3x - ) )
) )
⇔ 4cos( 5x +  )sin(
)sin( 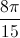 - 3x) = 2√3( cos
- 3x) = 2√3( cos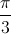 . sin( 3x -
. sin( 3x - ) – sin
) – sin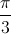 .cos(3x -
.cos(3x -  ))
))
⇔ 2cos(5x +  )sin(
)sin(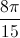 - 3x ) = √3sin( 3x -
- 3x ) = √3sin( 3x - 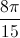 )
)
⇔ sin( 3x - 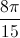 )[ 2cos( 5x +
)[ 2cos( 5x +  ) + √3] = 0
) + √3] = 0
⇔ 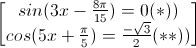
(*) 3x - 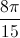 = kπ; k ∈ Z ⇔ x =
= kπ; k ∈ Z ⇔ x =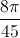 +
+ 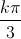 ; k ∈ Z.
; k ∈ Z.
(**) 5x +  = ±
= ±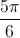 + m2π ; m∈ Z
+ m2π ; m∈ Z
⇔ 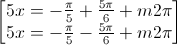 ⇔
⇔ 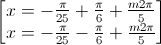
Vậy 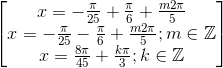
Phương trình đã cho tương đương với √3sin(3x -  ) + 2sin(8x -
) + 2sin(8x - 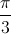 ) = 2sin(2x +
) = 2sin(2x + 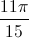 ) + 3cos(3x -
) + 3cos(3x -  )
)
⇔ 2sin(2x + 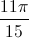 ) – 2sin(8x -
) – 2sin(8x - 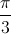 ) = √3sin(3x -
) = √3sin(3x -  ) – 3cos(3x -
) – 3cos(3x -  )
)
= √3( sin ( 3x -  ) – tan
) – tan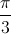 cos( 3x -
cos( 3x - ) )
) )
⇔ 4cos( 5x +  )sin(
)sin( 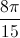 - 3x) = 2√3( cos
- 3x) = 2√3( cos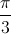 . sin( 3x -
. sin( 3x - ) – sin
) – sin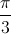 .cos(3x -
.cos(3x -  ))
))
⇔ 2cos(5x +  )sin(
)sin(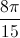 - 3x ) = √3sin( 3x -
- 3x ) = √3sin( 3x - 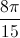 )
)
⇔ sin( 3x - 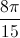 )[ 2cos( 5x +
)[ 2cos( 5x +  ) + √3] = 0
) + √3] = 0
⇔ 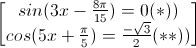
(*) 3x - 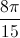 = kπ; k ∈ Z ⇔ x =
= kπ; k ∈ Z ⇔ x =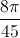 +
+ 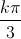 ; k ∈ Z.
; k ∈ Z.
(**) 5x +  = ±
= ±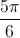 + m2π ; m∈ Z
+ m2π ; m∈ Z
⇔ 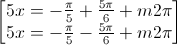 ⇔
⇔ 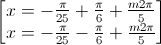
Vậy 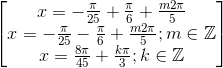
Câu hỏi liên quan
-

Tìm số phức z thỏa mãn
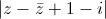 = √5 và (2 - z)(i +
= √5 và (2 - z)(i + 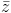 ) là số ảo.
) là số ảo. -

Cho các số thực x, y thỏa mãn điều kiện x+y=
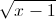 +
+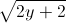 Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
P=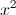 +
+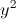 +2(x+1)(y+1)+8
+2(x+1)(y+1)+8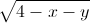
-

Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, BC = 2a. Gọi M là trung điểm của AC. Hình chiếu H của S lên mặt đáy (ABC) thuộc tia đối của tia MB sao cho MB = 2MH. Biết rằng góc giữa SA và mặt đáy (ABC) bằng 600. Tính thể tích khối chóp SABC và khoảng cách từ trung điểm E của SC tới (SAH).
-

Tìm nghiệm trong khoảng(0, π) của phương trình
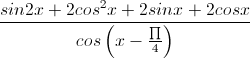 =
=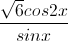
-

Giải hệ phương trình
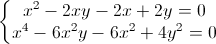 (x, y
(x, y R)
R) -

Tìm hệ số của x8 trong khai triển Niutơn của
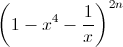 , biết rằng n thỏa mãn
, biết rằng n thỏa mãn 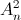 .
.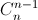 = 180. (
= 180. (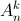 ,
, 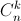 lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử).
lần lượt là số chỉnh hợp, số tổ hợp chập k của n phần tử). -

Tính tích phân I=
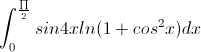
-

Giải phương trình (1-
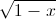 ).
).![\sqrt[3]{2-x}](https://luyentap365.com/wp-content/picture/learning/exam/2013/1031/75_220_2.gif) = x.
= x. -

Trong mặt phẳng với hệ trục Oxy, cho hai đường thẳng ∆1: 3x+y+5=0, ∆2: x-2y-3=0 và đường tròn (C):
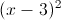 +
+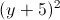 =25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2.
=25. Tìm điểm M thuộc (C), điểm N thuộc đường thẳng ∆1, sao cho M và N đối xứng qua ∆2. -

Tính tích phân I =