Giải hệ phương trình: 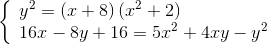

Câu hỏi
Nhận biếtGiải hệ phương trình: 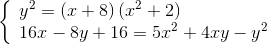
Đáp án đúng: A
Lời giải của Luyện Tập 365
Viết lại phương trình thứ hai của hệ về dạng
y2 –(4x-8)y + (16 +16x -5x2) = 0
Coi đây là phương trình bậc hai, ẩn là tham số. Có ∆’ = (2x+4)2 – (16+16x -5x2) = 9x2
Từ đó, tìm đượcy =4 –x ,y = 5x+4
Nếu y =4-x , thay vào phương trình thứ nhất, giải được x =0,x= -2 ,x= -5
V ới x = 0 th ì y= 4 –x =4
V ới x = -2 th ì y= 4 –x =6
V ới x = -5 th ì y= 4 –x =9
Nếu y =5x +4 , thay vào phương trình thứ nhất, giải được x =0,x= -2 ,x= 19
V ới x = 0 th ì y= 5x+4 =4
V ới x = -2 th ì y= 5x+4 = -6
V ới x = 19 th ì y= 5x+4 = 99
Vậy, các nghiệm của hệ là (x;y ) = (0;4),(-2;6),(-2;-6) , (-5;9), (19;99)
Viết lại phương trình thứ hai của hệ về dạng
y2 –(4x-8)y + (16 +16x -5x2) = 0
Coi đây là phương trình bậc hai, ẩn là tham số. Có ∆’ = (2x+4)2 – (16+16x -5x2) = 9x2
Từ đó, tìm đượcy =4 –x ,y = 5x+4
Nếu y =4-x , thay vào phương trình thứ nhất, giải được x =0,x= -2 ,x= -5
V ới x = 0 th ì y= 4 –x =4
V ới x = -2 th ì y= 4 –x =6
V ới x = -5 th ì y= 4 –x =9
Nếu y =5x +4 , thay vào phương trình thứ nhất, giải được x =0,x= -2 ,x= 19
V ới x = 0 th ì y= 5x+4 =4
V ới x = -2 th ì y= 5x+4 = -6
V ới x = 19 th ì y= 5x+4 = 99
Vậy, các nghiệm của hệ là (x;y ) = (0;4),(-2;6),(-2;-6) , (-5;9), (19;99)
Câu hỏi liên quan
-

Tìm a để phương trình có 2 nghiệm nguyên
-

Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-

Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-

Giải phương trình với a = -2
-

Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Tính AC và BD biết
 =
=  . Chứng tỏ tích AC.BD không phụ thuộc vào
. Chứng tỏ tích AC.BD không phụ thuộc vào 
-

Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-

Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-

Rút gọn A
-

Tìm m để phương trình (1) có nghiệm .
