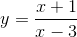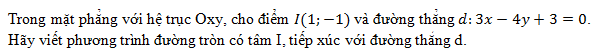Giải bất phương trình \(\sqrt {{x^2} - 3x + 2} + \sqrt {{x^2} - 4x + 3} \ge 2\sqrt {{x^2} - 5x + 4} \) .
Câu hỏi
Nhận biếtGiải bất phương trình \(\sqrt {{x^2} - 3x + 2} + \sqrt {{x^2} - 4x + 3} \ge 2\sqrt {{x^2} - 5x + 4} \) .
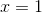
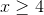
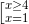
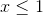
Đáp án đúng: C
Phương pháp giải
+) Tìm điều kiện xác định.
+) Đối với mỗi trường hợp của x, đưa phương trình về dạng tích sao cho hợp lí.
+) Tìm điều kiện xác định.
+) Đối với mỗi trường hợp của x, đưa phương trình về dạng tích sao cho hợp lí.
Lời giải của Luyện Tập 365
Điều kiện: \(\left\{ \begin{array}{l}{x^2} - 3x + 2 \ge 0\\{x^2} - 4x + 3 \ge 0\\{x^2} - 5x + 4 \ge 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 4\\x \le 1\end{array} \right.\)
TH1: Nếu \(x \ge 4\), khi đó:
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow \sqrt {\left( {x - 1} \right)\left( {x - 2} \right)} + \sqrt {\left( {x - 1} \right)\left( {x - 3} \right)} \ge 2\sqrt {\left( {x - 1} \right)\left( {x - 4} \right)} \\ \Leftrightarrow \sqrt {x - 2} + \sqrt {x - 3} \ge 2\sqrt {x - 4} \\ \Leftrightarrow \sqrt {x - 2} - \sqrt {x - 4} \ge \sqrt {x - 4} - \sqrt {x - 3} \end{array}\)
(luôn đúng vì VT > 0, VP < 0 với mọi \(x \ge 4\)).
Vậy \(x \ge 4\) là nghiệm của bất phương trình.
TH2: Nếu \(x \le 1\), khi đó:
\(\left( 1 \right) \Leftrightarrow \sqrt {\left( {1 - x} \right)\left( {2 - x} \right)} + \sqrt {\left( {1 - x} \right)\left( {3 - x} \right)} \ge 2\sqrt {\left( {1 - x} \right)\left( {4 - x} \right)} \)
Với \(x = 1\) thì \(0 + 0 \ge 0\) (đúng) \( \Rightarrow x = 1\) là nghiệm của bất phương trình.
Với \(x < 1\), bất phương trình có dạng:
\(\sqrt {2 - x} - \sqrt {4 - x} \ge \sqrt {4 - x} - \sqrt {3 - x} \)
Nhận xét: VT < 0, VP > 0 \(\forall x < 1\), do đó bất phương trình vô nghiệm.
Vậy bất phương trình có nghiệm duy nhất \(x = 1\).
Điều kiện: \(\left\{ \begin{array}{l}{x^2} - 3x + 2 \ge 0\\{x^2} - 4x + 3 \ge 0\\{x^2} - 5x + 4 \ge 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 4\\x \le 1\end{array} \right.\)
TH1: Nếu \(x \ge 4\), khi đó:
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow \sqrt {\left( {x - 1} \right)\left( {x - 2} \right)} + \sqrt {\left( {x - 1} \right)\left( {x - 3} \right)} \ge 2\sqrt {\left( {x - 1} \right)\left( {x - 4} \right)} \\ \Leftrightarrow \sqrt {x - 2} + \sqrt {x - 3} \ge 2\sqrt {x - 4} \\ \Leftrightarrow \sqrt {x - 2} - \sqrt {x - 4} \ge \sqrt {x - 4} - \sqrt {x - 3} \end{array}\)
(luôn đúng vì VT > 0, VP < 0 với mọi \(x \ge 4\)).
Vậy \(x \ge 4\) là nghiệm của bất phương trình.
TH2: Nếu \(x \le 1\), khi đó:
\(\left( 1 \right) \Leftrightarrow \sqrt {\left( {1 - x} \right)\left( {2 - x} \right)} + \sqrt {\left( {1 - x} \right)\left( {3 - x} \right)} \ge 2\sqrt {\left( {1 - x} \right)\left( {4 - x} \right)} \)
Với \(x = 1\) thì \(0 + 0 \ge 0\) (đúng) \( \Rightarrow x = 1\) là nghiệm của bất phương trình.
Với \(x < 1\), bất phương trình có dạng:
\(\sqrt {2 - x} - \sqrt {4 - x} \ge \sqrt {4 - x} - \sqrt {3 - x} \)
Nhận xét: VT < 0, VP > 0 \(\forall x < 1\), do đó bất phương trình vô nghiệm.
Vậy bất phương trình có nghiệm duy nhất \(x = 1\).
Câu hỏi liên quan
-
Phần cơ bản
-
-
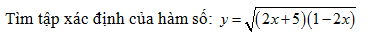
Dùng định nghĩa tìm khoảng tăng giảm của hàm số:
-
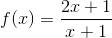
Giải và biện luận phương trình sau theo tham số m
-
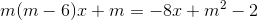
Tìm miền xác định của hàm số sau:
-
Cho a,b,c là số thực dương. Chứng minh rằng:
-
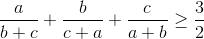
. Cho tam giác ABC với A(-1;2);B(-2;5);C(0;-3).
a) Tính tọa độ trọng tâm G của tam giác ABC.
b) Tìm tọa độ điểm D sao cho tứ giác ADBC là hình bình hành
-
Tìm tập xác định của hàm số sau;
a)
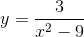
b)
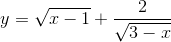
c)
-
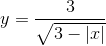
Cho góc
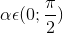thỏa mãn 
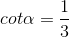. Tính các giá trị lượng giác của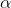 
-
Dùng định nghĩa để tìm khảng tăng giảm của hàm số
