Giả sử đường thẳng MN cắt các tia AB, AC lần lượt tại các điểm Q, R. Qua R kẻ đường thẳng tiếp xúc với (O) cắt tia AB tại điểm S; qua Q kẻ đường thẳng tiếp xúc với (O') cắt tia AC tại điểm T. Chứng minh rằng tứ giác QSRT ngoại tiếp được.
Câu hỏi
Nhận biếtGiả sử đường thẳng MN cắt các tia AB, AC lần lượt tại các điểm Q, R. Qua R kẻ đường thẳng tiếp xúc với (O) cắt tia AB tại điểm S; qua Q kẻ đường thẳng tiếp xúc với (O') cắt tia AC tại điểm T. Chứng minh rằng tứ giác QSRT ngoại tiếp được.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Gọi I, K theo thứ tự là tiếp điểm của RS với (O); của QT với (O').
Ta có: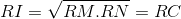 
; 
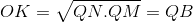
Suy ra RS + QT = SI + IR + QK + KT = SB + RC + QB + CT = SQ + RT
=> đpcm.
Gọi I, K theo thứ tự là tiếp điểm của RS với (O); của QT với (O').
Ta có: ;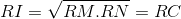
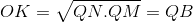
Suy ra RS + QT = SI + IR + QK + KT = SB + RC + QB + CT = SQ + RT
=> đpcm.
Câu hỏi liên quan
-
AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-
Giải hệ phương trình với a = 2
-
Chứng minh rằng: AM2 = AN.AB
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-
Tính AC và BD biết
= 
. Chứng tỏ tích AC.BD không phụ thuộc vào -
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Chứng minh DM.CE=DE.CM
-
Tìm b để A =
-
Tìm a để phương trình có 2 nghiệm nguyên
-
Cho biểu thức:
A =
Trả lời câu hỏi dưới đây:
Rút gọn A