Đường thẳng AD cắt đường tròn đường kính MC tại N (N khác D). Đường thẳng MD cắt CN tại K, MN cắt CD tại H. Chứng minh KH song song với NE.
Câu hỏi
Nhận biếtĐường thẳng AD cắt đường tròn đường kính MC tại N (N khác D). Đường thẳng MD cắt CN tại K, MN cắt CD tại H. Chứng minh KH song song với NE.
Đáp án đúng: D
Lời giải của Luyện Tập 365
Trong tam giác MKC có MN ⊥KC; CD ⊥MK suy ra H là trực tâm của tam giác MKC.
=> KH ⊥MC hay KH ⊥AC
=> KH//AB(cùng vuông góc với AC) (1)
Ta có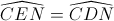 
(hai góc nội tiếp cùng chắn cung CN của đường tròn đường kính MC)
Mà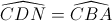 
(cùng bù với góc )
=> 
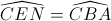=> EB//BA (2)
Từ (1) và (2) suy ra KH // EN.
Trong tam giác MKC có MN ⊥KC; CD ⊥MK suy ra H là trực tâm của tam giác MKC.
=> KH ⊥MC hay KH ⊥AC
=> KH//AB(cùng vuông góc với AC) (1)
Ta có 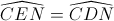(hai góc nội tiếp cùng chắn cung CN của đường tròn đường kính MC)
Mà 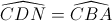(cùng bù với góc )
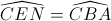=> => EB//BA (2)
Từ (1) và (2) suy ra KH // EN.
Câu hỏi liên quan
-
Tìm b để A =
-
Rút gọn biểu thức A
-
Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-
Giải hệ phương trình với a = 2
-
Cho biểu thức A = (
- 
+ 
) : ( x - 2 + 
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-
Tìm m để phương trình (1) có nghiệm .
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Giải phương trình với a = -2
-
Cho biểu thức:
A =
Trả lời câu hỏi dưới đây:
Rút gọn A
-
Giải hệ phương trình
