Chứng minh rằng với các số dương a và b: Trả lời câu hỏi dưới đây:Nếu a < b thì 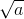 <
< 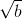 và ngược lại.
và ngược lại.

Câu hỏi
Nhận biếtChứng minh rằng với các số dương a và b:
Trả lời câu hỏi dưới đây:
Nếu a < b thì 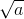 <
< 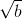 và ngược lại.
và ngược lại.
Đáp án đúng: A
Lời giải của Luyện Tập 365
0 < a < b nên a - b < 0 => 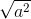 -
- 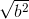 < 0
< 0
<=> (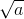 -
- 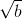 )(
)(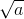 +
+ 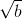 ) < 0
) < 0
<=> 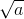 -
- 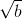 < 0 (do
< 0 (do 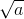 +
+ 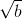 > 0)
> 0)
<=> 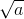 <
< 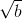
Ngược lại với a > 0, b > 0, 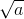 <
< 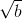 <=>
<=> 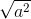 -
- 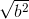 < 0
< 0
<=> (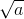 -
- 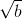 )(
)(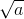 +
+ 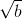 ) < 0 <=> a - b < 0
) < 0 <=> a - b < 0
<=> a < b
0 < a < b nên a - b < 0 => 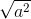 -
- 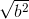 < 0
< 0
<=> (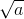 -
- 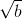 )(
)(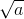 +
+ 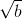 ) < 0
) < 0
<=> 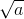 -
- 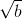 < 0 (do
< 0 (do 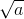 +
+ 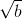 > 0)
> 0)
<=> 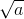 <
< 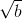
Ngược lại với a > 0, b > 0, 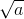 <
< 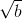 <=>
<=> 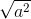 -
- 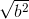 < 0
< 0
<=> (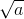 -
- 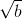 )(
)(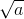 +
+ 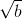 ) < 0 <=> a - b < 0
) < 0 <=> a - b < 0
<=> a < b
Câu hỏi liên quan
-

Tìm m để phương trình (1) có nghiệm .
-

Giải hệ phương trình

-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Tìm a để phương trình có 2 nghiệm nguyên
-

Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Tính AC và BD biết
 =
=  . Chứng tỏ tích AC.BD không phụ thuộc vào
. Chứng tỏ tích AC.BD không phụ thuộc vào 
-

Rút gọn biểu thức A
-

Chứng minh rằng: AM2 = AN.AB
-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
