Chứng minh rằng:
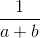 +
+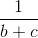 +
+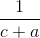 +
+![\frac{1}{2\sqrt[3]{abc}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/52900_197152_4.gif) ≥
≥ ![\frace_{{\left( {a + b + c + \sqrt[3]{{abc} \right)}^2}}}e_(a + b)(b + c)(c + a)](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/52900_917814_5.gif) với mọi a, b, c > 0
với mọi a, b, c > 0

Câu hỏi
Nhận biếtChứng minh rằng:
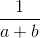 +
+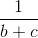 +
+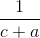 +
+![\frac{1}{2\sqrt[3]{abc}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/52900_197152_4.gif) ≥
≥ ![\frace_{{\left( {a + b + c + \sqrt[3]{{abc} \right)}^2}}}e_(a + b)(b + c)(c + a)](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/52900_917814_5.gif) với mọi a, b, c > 0
với mọi a, b, c > 0
Đáp án đúng: A
Lời giải của Luyện Tập 365
Bất đẳng thức cần chứng minh tương đương với
(a+b)(b+c)(c+a)(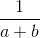 +
+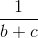 +
+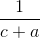 +
+![\frac{1}{2\sqrt[3]{abc}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_45035_4.gif) ) ≥ (+b+c+2
) ≥ (+b+c+2![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_972122_5.gif) )2.
)2.
Chứng minh : (a+b)(b+c)(c+a) =c2(a+b)+a2(b+c) +b2(c+a)+2abc
Áp dụng bất đẳng thức Cauchy -Bunhiacopsky -Schwarz :
(c2(a+b)+a2(b+c) +b2(c+a)+2abc) (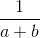 +
+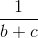 +
+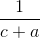 +
+![\frac{1}{2\sqrt[3]{abc}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_45035_4.gif) ) ≥
) ≥
(c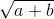 .
.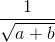 +a
+a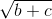 .
.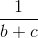 +b
+b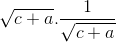 +
+ ![{\sqrt {2abc} .\sqrt {\frac{1}e_2\sqrt[3]{{abc}}} }](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_384644_15.gif) )2 = (c+a+b +
)2 = (c+a+b + ![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_972122_5.gif) )2.
)2.
Dấu “ = ” xảy ra khi và chỉ khi c(a+b)=a(c+a) = b(c+a) = 2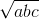 .
.![\sqrt[6]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_205357_18.gif)
< => a=b=c
Bất đẳng thức cần chứng minh tương đương với
(a+b)(b+c)(c+a)(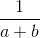 +
+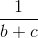 +
+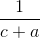 +
+![\frac{1}{2\sqrt[3]{abc}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_45035_4.gif) ) ≥ (+b+c+2
) ≥ (+b+c+2![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_972122_5.gif) )2.
)2.
Chứng minh : (a+b)(b+c)(c+a) =c2(a+b)+a2(b+c) +b2(c+a)+2abc
Áp dụng bất đẳng thức Cauchy -Bunhiacopsky -Schwarz :
(c2(a+b)+a2(b+c) +b2(c+a)+2abc) (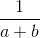 +
+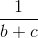 +
+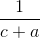 +
+![\frac{1}{2\sqrt[3]{abc}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_45035_4.gif) ) ≥
) ≥
(c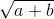 .
.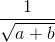 +a
+a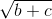 .
.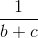 +b
+b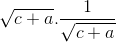 +
+ ![{\sqrt {2abc} .\sqrt {\frac{1}e_2\sqrt[3]{{abc}}} }](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_384644_15.gif) )2 = (c+a+b +
)2 = (c+a+b + ![\sqrt[3]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_972122_5.gif) )2.
)2.
Dấu “ = ” xảy ra khi và chỉ khi c(a+b)=a(c+a) = b(c+a) = 2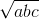 .
.![\sqrt[6]{abc}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0423/v48330_205357_18.gif)
< => a=b=c
Câu hỏi liên quan
-

Rút gọn biểu thức A
-

Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-

Chứng minh rằng: AM2 = AN.AB
-

Tính AC và BD biết
 =
=  . Chứng tỏ tích AC.BD không phụ thuộc vào
. Chứng tỏ tích AC.BD không phụ thuộc vào 
-

Giải hệ phương trình với a = 2
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Tìm b để A =

-

Giải phương trình (1) khi m = -5
-

Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
