Chứng minh: KF // CD.
Câu hỏi
Nhận biếtChứng minh: KF // CD.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Vì ∆ NEC cân tại N có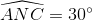 
nên 
.
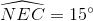∆ ABC cân tại A mà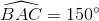 
=> 
=> 
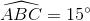
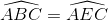hay tứ giác ABEC nội tiếp.
=> 
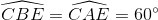
Kết hợp với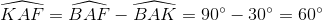 
, ta có tứ giác ABKF nội tiếp.
Mặt khác: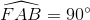 
nên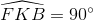 
hay FK ┴ BE.
Do tứ giác ABEC nội tiếp nên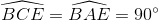 
.
Tam giác vuông BCE có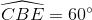 
nên BE = 2 BC.
Lại có: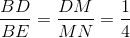 
=> 
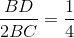=> BC = 2 BD
=> ∆ BDC ~ ∆ BCE.
Do đó: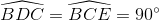 
hay CD ┴ BE
Vậy KF // CD.
Vì ∆ NEC cân tại N có 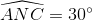nên .
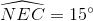∆ ABC cân tại A mà =>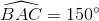
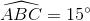
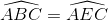=> hay tứ giác ABEC nội tiếp.
=>
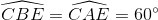
Kết hợp với 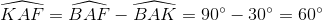, ta có tứ giác ABKF nội tiếp.
Mặt khác: 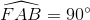nên 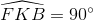hay FK ┴ BE.
Do tứ giác ABEC nội tiếp nên .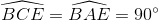
Tam giác vuông BCE có 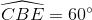nên BE = 2 BC.
Lại có: 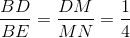=> => 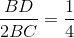BC = 2 BD
=> ∆ BDC ~ ∆ BCE.
Do đó: 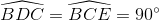hay CD ┴ BE
Vậy KF // CD.
Câu hỏi liên quan
-
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Cho nửa đường tròn (O), đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E khắc với điểm A. Từ các điểm E, A và B kẻ các tiếp tuyến của nửa đường tròn (O). Tiếp tuyến kẻ từ E lần lượt cắt các tiếp tuyến từ điểm A và B tại C và D.
Trả lời câu hỏi dưới đây:
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-
Rút gọn biểu thức A
-
Chứng minh DM.CE=DE.CM
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Giải phương trình với a = -2
-
Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.