Chứng minh H1 nằm trên đường tròn (O)
Câu hỏi
Nhận biếtChứng minh H1 nằm trên đường tròn (O)
Đáp án đúng: A
Lời giải của Luyện Tập 365
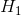đối xứng với H qua BC nên 
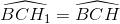mà 
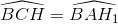(góc có cạnh tương ứng vuông góc) suy ra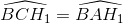 
Tứ giác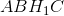 
nội tiếp đường tròn
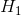=> ϵ (O)
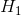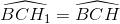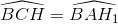đối xứng với H qua BC nên mà (góc có cạnh tương ứng vuông góc) suy ra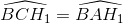
Tứ giác 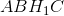nội tiếp đường tròn
=> ϵ (O)
Câu hỏi liên quan
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Tìm m để phương trình (1) có nghiệm .
-
Giải phương trình với a = -2
-
Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-
Giải hệ phương trình
-
Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-
Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-
Tính AC và BD biết
= 
. Chứng tỏ tích AC.BD không phụ thuộc vào