Chứng minh BC là tia phân giác của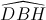 
và tứ giác BDCH là hình thoi.
Câu hỏi
Nhận biếtChứng minh BC là tia phân giác của 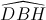và tứ giác BDCH là hình thoi.
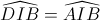
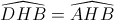
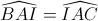
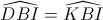
Đáp án đúng: D
Lời giải của Luyện Tập 365
Ta có ∆ABC cân tại A (gt), AI là đường cao nên AI là tia phân giác của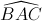 
=> 
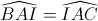
Mà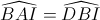 
(hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
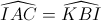(hai góc nội tiếp chắn cung KI)
Do đó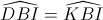 
Vậy BC là tia phân giác của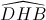 
∆BHD có BI là đường phân giác và là đường cao nên ∆BHD cân tại B => BI là đường trung tuyến => IH = ID
Tứ giác BDCH có I là trung điểm của BC, HD nên tứ giác BDCH là hình bình hành.
Mà HD⊥BC.
Vậy tứ giác BHCD là hình thoi.
Ta có ∆ABC cân tại A (gt), AI là đường cao nên AI là tia phân giác của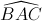
=>
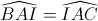
Mà 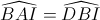(hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
(hai góc nội tiếp chắn cung KI)
Do đó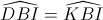
Vậy BC là tia phân giác của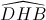
∆BHD có BI là đường phân giác và là đường cao nên ∆BHD cân tại B => BI là đường trung tuyến => IH = ID
Tứ giác BDCH có I là trung điểm của BC, HD nên tứ giác BDCH là hình bình hành.
Mà HD⊥BC.
Vậy tứ giác BHCD là hình thoi.
Câu hỏi liên quan
-
Cho nửa đường tròn (O), đường kính AB = 2R. Trên tia đối của tia AB lấy điểm E khắc với điểm A. Từ các điểm E, A và B kẻ các tiếp tuyến của nửa đường tròn (O). Tiếp tuyến kẻ từ E lần lượt cắt các tiếp tuyến từ điểm A và B tại C và D.
Trả lời câu hỏi dưới đây:
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-
Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-
Giải hệ phương trình
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Tính giá trị biểu thức của A với x =
-
Chứng minh rằng: AM2 = AN.AB
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Rút gọn biểu thức A
-
Cho biểu thức A = (
- 
+ 
) : ( x - 2 + 
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A