Chứng minh AC là tiếp tuyến của đường tròn (O)
Câu hỏi
Nhận biếtChứng minh AC là tiếp tuyến của đường tròn (O)
A.
Xem phần lời giải
Đáp án đúng: A
Lời giải của Luyện Tập 365
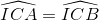vì CI là phân giác của góc ACB
∆ OIC cân ở O nên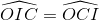 
mà 
=> 
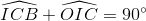
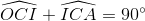hay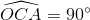 
nên AC ┴ OC
Vậy AC là tiếp tuyến của đường tròn (O)
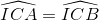vì CI là phân giác của góc ACB
∆ OIC cân ở O nên 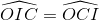mà
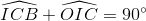
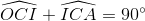=> hay 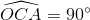nên AC ┴ OC
Vậy AC là tiếp tuyến của đường tròn (O)
Câu hỏi liên quan
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Tính giá trị biểu thức của A với x =
-
Rút gọn biểu thức A
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Tìm m để phương trình (1) có nghiệm .
-
Giải phương trình với a = -2
-
Tính AC và BD biết
= 
. Chứng tỏ tích AC.BD không phụ thuộc vào -
Chứng minh rằng: AM2 = AN.AB
-
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.