Cho tứ diện ABCD với M ; N là trung điểm của AB và CD . Gọi G là trọng tâm của tứ diện . Chứng minh : \(\eqalign{ & a)\,\,2\overrightarrow {MN} = \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {AC} + \overrightarrow {BD} \cr & b)\,\,\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \cr & c)\,\,\forall I:\,\,4\overrightarrow {IG} = \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} \cr} \)

Câu hỏi
Nhận biếtCho tứ diện ABCD với M ; N là trung điểm của AB và CD . Gọi G là trọng tâm của tứ diện . Chứng minh :
\(\eqalign{
& a)\,\,2\overrightarrow {MN} = \overrightarrow {AD} + \overrightarrow {BC} + \overrightarrow {AC} + \overrightarrow {BD} \cr
& b)\,\,\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \cr
& c)\,\,\forall I:\,\,4\overrightarrow {IG} = \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} \cr} \)
Đáp án đúng:
Lời giải của Luyện Tập 365
a)
Áp dụng qui tắc 3 điểm ta có :
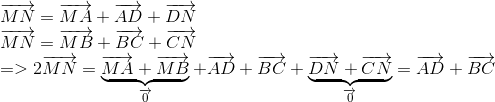
Chứng minh tương tự ta có : 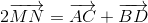
b) Áp dụng qui tắc trung điểm ta có :
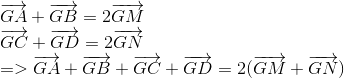
Vì G là trọng tâm tứ diện nên :
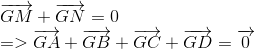
c) Với mọi điểm I trong không gian , áp dụng qui tắc 3 điểm :
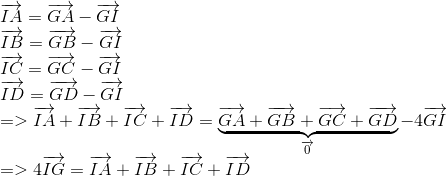
a)
Áp dụng qui tắc 3 điểm ta có :
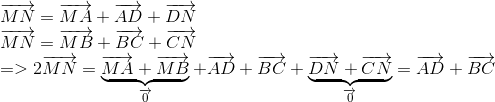
Chứng minh tương tự ta có : 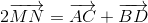
b) Áp dụng qui tắc trung điểm ta có :
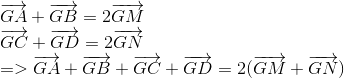
Vì G là trọng tâm tứ diện nên :
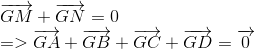
c) Với mọi điểm I trong không gian , áp dụng qui tắc 3 điểm :
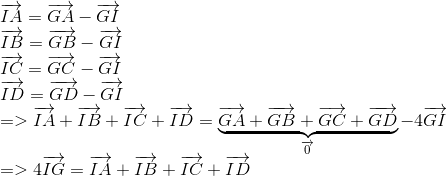
Câu hỏi liên quan
-

Có bao nhiêu cách sắp xếp 5 bạn học sinh A, B, C, D, E ngồi vào một chiếc ghế dài sao cho:
a. Bạn C ngồi chính giữa?
b. Hai bạn A và E ngồi ở hai đầu ghế?
-

: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn).
a) Xác định giao tuyến của hai cặp mặt phẳng (SAC) và (SBD) ;(SAD) và (SBC).
b) M là một điểm trên cạnh SC không trùng với S và C. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (ABM).
c) Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC), chứng minh d và BM đồng phẳng.
-

-

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 8.
b) Tích số chấm hai mặt xuất hiện là số lẻ.
-

Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?
-

-

Giải các phương trình sau:
a)
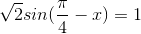
b)
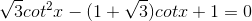
-

-

Giải các phương trình sau:
a)
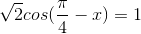
b)
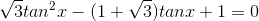
-

Có bao nhiêu cách xếp chỗ cho 5 người vào 5 ghế ngồi xung quanh một bàn tròn, nếu không có sự phân biệt giữa các ghế này?