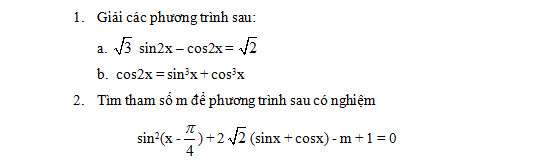Cho tứ diện \(ABCD\) có: \(SA = SB = SC = AB = AC = a\) và \(BC = a\sqrt 2 \). Tính góc: \(\left( {\overrightarrow {AB} ;\overrightarrow {SC} } \right)\).

Câu hỏi
Nhận biếtCho tứ diện \(ABCD\) có: \(SA = SB = SC = AB = AC = a\) và \(BC = a\sqrt 2 \). Tính góc: \(\left( {\overrightarrow {AB} ;\overrightarrow {SC} } \right)\).
Đáp án đúng:
Lời giải của Luyện Tập 365
Theo giả thiết ta có :
\(\Delta SAB = \Delta SAC\) ( 2 tam giác đều)
\(\Delta SBC = \Delta ABC\) ( 2 tam giác vuông tại S và tại A)
\(\eqalign{
& \cos \left( {\overrightarrow {AB} ;\overrightarrow {SC} } \right) = {{\overrightarrow {AB} .\overrightarrow {SC} } \over {AB.SC}} = {{\overrightarrow {AB} \left( {\overrightarrow {AC} - \overrightarrow {AS} } \right)} \over {AB.SC}} \cr
& = {{\overrightarrow {AB} .\overrightarrow {AC} - \overrightarrow {AB} .\overrightarrow {AS} } \over {{a^2}}} = {{ - \overrightarrow {AB} .\overrightarrow {AS} } \over {{a^2}}} = {{ - {a^2}\cos {{60}^0}} \over {{a^2}}} = - {1 \over 2} \cr
& \Rightarrow \left( {\overrightarrow {AB} ;\overrightarrow {SC} } \right) = {120^0} \cr} \)
Theo giả thiết ta có :
\(\Delta SAB = \Delta SAC\) ( 2 tam giác đều)
\(\Delta SBC = \Delta ABC\) ( 2 tam giác vuông tại S và tại A)
\(\eqalign{
& \cos \left( {\overrightarrow {AB} ;\overrightarrow {SC} } \right) = {{\overrightarrow {AB} .\overrightarrow {SC} } \over {AB.SC}} = {{\overrightarrow {AB} \left( {\overrightarrow {AC} - \overrightarrow {AS} } \right)} \over {AB.SC}} \cr
& = {{\overrightarrow {AB} .\overrightarrow {AC} - \overrightarrow {AB} .\overrightarrow {AS} } \over {{a^2}}} = {{ - \overrightarrow {AB} .\overrightarrow {AS} } \over {{a^2}}} = {{ - {a^2}\cos {{60}^0}} \over {{a^2}}} = - {1 \over 2} \cr
& \Rightarrow \left( {\overrightarrow {AB} ;\overrightarrow {SC} } \right) = {120^0} \cr} \)
Câu hỏi liên quan
-

Gieo hai con súc sắc cân đối đồng chất. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 7.
b) Các mặt xuất hiện có số chấm bằng nhau.
-

-

Giải các phương trình sau:
a)
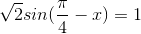
b)
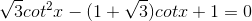
-

-

-

Tìm số hạng không chứa x trong khai triển của nhị thức
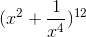
-

Tìm tập xác định của các hàm số sau:
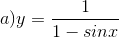
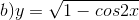
-

Có bao nhiêu cách sắp xếp 5 bạn học sinh A, B, C, D, E ngồi vào một chiếc ghế dài sao cho:
a. Bạn C ngồi chính giữa?
b. Hai bạn A và E ngồi ở hai đầu ghế?
-

Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?
-