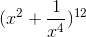Cho tứ diện ABCD có I là trung điểm cạnh AB , G là trong tâm của tam giác ACD và J là 1điểm tùy ý trên cạnh BC sao cho IJ không song song với AC. Xác định :
a)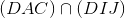
b) Tìm giao tuyến của mặt phẳng (IJG) và các mặt phẳng (ACD) ; (BCD) ; (ABD)
Câu hỏi
Nhận biếtCho tứ diện ABCD có I là trung điểm cạnh AB , G là trong tâm của tam giác ACD và J là 1điểm tùy ý trên cạnh BC sao cho IJ không song song với AC. Xác định :
a)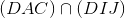
b) Tìm giao tuyến của mặt phẳng (IJG) và các mặt phẳng (ACD) ; (BCD) ; (ABD)
Đáp án đúng:
Lời giải của Luyện Tập 365
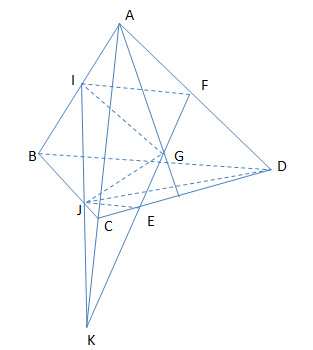
a) Ta có :
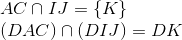
b) Ta có :
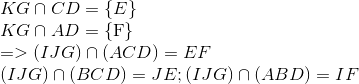
a) Ta có :
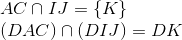
b) Ta có :
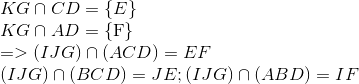
Câu hỏi liên quan
-
Có bao nhiêu cách xếp chỗ cho 5 người vào 5 ghế ngồi xung quanh một bàn tròn, nếu không có sự phân biệt giữa các ghế này?
-
-
-
Tìm tập xác định của các hàm số sau:
-
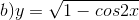
: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn).
a) Xác định giao tuyến của hai cặp mặt phẳng (SAC) và (SBD) ;(SAD) và (SBC).
b) M là một điểm trên cạnh SC không trùng với S và C. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (ABM).
c) Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC), chứng minh d và BM đồng phẳng.
-
Tìm số hạng không chứa x trong khai triển của nhị thức
-
-
-
-
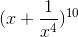
Tìm số hạng không chứa x trong khai triển của nhị thức
