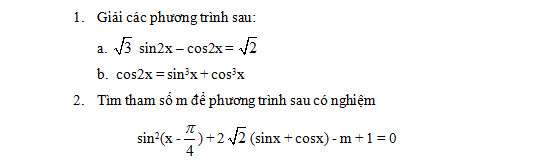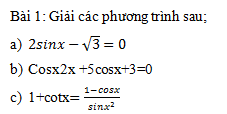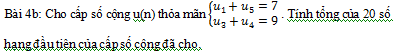Cho tứ diện ABCD có DA vuông góc với (ABC) và AI vuông góc với BC. Gọi H là trực tâm của tam giác ABC . Kẻ HK vuông góc với DI. Chứng minh HK vuông góc với (DBC) và K là trực tâm của tam giác DBC.

Câu hỏi
Nhận biếtCho tứ diện ABCD có DA vuông góc với (ABC) và AI vuông góc với BC. Gọi H là trực tâm của tam giác ABC . Kẻ HK vuông góc với DI. Chứng minh HK vuông góc với (DBC) và K là trực tâm của tam giác DBC.
Đáp án đúng:
Lời giải của Luyện Tập 365

Ta có :
\(\eqalign{
& \left\{ \matrix{
DA \bot \left( {ABCD} \right) \Rightarrow DA \bot BC \hfill \cr
AI \bot BC \hfill \cr} \right. \Rightarrow BC \bot \left( {DAI} \right) \Rightarrow \left( {DBC} \right) \bot \left( {DAI} \right) \cr
& \Rightarrow HK \bot \left( {DBC} \right) \Rightarrow HK \bot DC \cr
& \left\{ \matrix{
DA \bot \left( {ABC} \right) \Rightarrow DA \bot BH \hfill \cr
AC \bot BH \hfill \cr} \right. \Rightarrow BH \bot \left( {DAC} \right) \Rightarrow BH \bot DC \cr
& \Rightarrow DC \bot \left( {BHK} \right) \Rightarrow DC \bot BK \cr} \)
Vậy K là trực tâm tam giác DBC

Ta có :
\(\eqalign{
& \left\{ \matrix{
DA \bot \left( {ABCD} \right) \Rightarrow DA \bot BC \hfill \cr
AI \bot BC \hfill \cr} \right. \Rightarrow BC \bot \left( {DAI} \right) \Rightarrow \left( {DBC} \right) \bot \left( {DAI} \right) \cr
& \Rightarrow HK \bot \left( {DBC} \right) \Rightarrow HK \bot DC \cr
& \left\{ \matrix{
DA \bot \left( {ABC} \right) \Rightarrow DA \bot BH \hfill \cr
AC \bot BH \hfill \cr} \right. \Rightarrow BH \bot \left( {DAC} \right) \Rightarrow BH \bot DC \cr
& \Rightarrow DC \bot \left( {BHK} \right) \Rightarrow DC \bot BK \cr} \)
Vậy K là trực tâm tam giác DBC
Câu hỏi liên quan
-

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 8.
b) Tích số chấm hai mặt xuất hiện là số lẻ.
-

-

Có bao nhiêu cách xếp chỗ cho 5 người vào 5 ghế ngồi xung quanh một bàn tròn, nếu không có sự phân biệt giữa các ghế này?
-

-

Một hộp kín chứa 2 quả cầu màu trắng và 8 quả màu đen, các quả cầu chỉ khác nhau về màu sắc.
a) Lấy ngẫu nhiên 3 quả cầu từ hộp đã cho. Tính xác suất để lấy được ba quả cầu cùng màu.
b) Lấy ngẫu nhiên các quả cầu từ hộp đã cho hai lần như sau: Lần thứ nhất lấy ra 3 quả cầu rồi trả lại vào hộp. Lần thứ 3 lấy ra 3 quả cầu. Tính xác suất để số cầu trắng của hai lần lấy là như nhau.
-


bai 3 de 2 HK1 minh khai ha tinh 13-14
-

-

Có bao nhiêu cách sắp xếp 5 bạn học sinh A, B, C, D, E ngồi vào một chiếc ghế dài sao cho:
a. Bạn C ngồi chính giữa?
b. Hai bạn A và E ngồi ở hai đầu ghế?
-

-