Cho tam giác nhọn ABC có AB = b, AC = c. M là một điểm thay đổi trên cạnh AB. Đường tròn ngoại tiếp tam giác BMC cắt các cạnh AC tại N. Trả lời câu hỏi dưới đây:Gọi I là tâm đường tròn ngoại tiếp tam giác AMN. Chứng minh I luôn thuộc một đường thẳng cố định.
Câu hỏi
Nhận biếtCho tam giác nhọn ABC có AB = b, AC = c. M là một điểm thay đổi trên cạnh AB. Đường tròn ngoại tiếp tam giác BMC cắt các cạnh AC tại N.
Trả lời câu hỏi dưới đây:
Gọi I là tâm đường tròn ngoại tiếp tam giác AMN. Chứng minh I luôn thuộc một đường thẳng cố định.
Đáp án đúng: B
Lời giải của Luyện Tập 365
Vẽ Ax là tiếp tuyến của đường tròn (I)
Ta có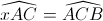 
=> Ax // BC (Hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
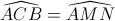
Nên 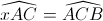=> Ax //BC
Mà IA ⊥Ax (Ax là tia tiếp tuyến của đường tròn (I))
Do đó IA ⊥BC
Vậy I thuộc đường thẳng cố định qua A và vuông góc với BC.
Vẽ Ax là tiếp tuyến của đường tròn (I)
Ta có 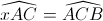=> Ax // BC (Hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
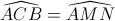
Nên 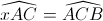=> Ax //BC
Mà IA ⊥Ax (Ax là tia tiếp tuyến của đường tròn (I))
Do đó IA ⊥BC
Vậy I thuộc đường thẳng cố định qua A và vuông góc với BC.
Câu hỏi liên quan
-
Chứng minh rằng: AM2 = AN.AB
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-
Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-
Giải hệ phương trình
-
Chứng minh DM.CE=DE.CM
-
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Tìm b để A =
-
Rút gọn biểu thức A