Cho tam giác có số đo của một góc bằng trung bình cộng của số đo hai góc còn lại và độ dài các cạnh a, b, c của tam giác đó thỏa mãn: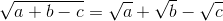 
. Chứng minh rằng tam giác này là tam giác đều.
Câu hỏi
Nhận biếtCho tam giác có số đo của một góc bằng trung bình cộng của số đo hai góc còn lại và độ dài các cạnh a, b, c của tam giác đó thỏa mãn: 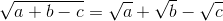. Chứng minh rằng tam giác này là tam giác đều.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Từ giả thiết số đo một góc bằng trung bình cộng số đo hai góc còn lại, suy ra tam giác đã cho có ít nhất một góc bằng 60°.
Ví dụ: Từ 2A = B + C suy ra 3A = A + B + C = 180°. Do đó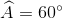 
Từ 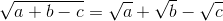(*) , suy ra tam giác đã cho là tam giác cân.
Thật vậy, bình phương các vế của (*):
a + b - c = a + b + c +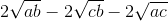 
=> 
=> 
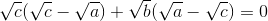
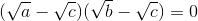
Vậy tam giác này có a = c hoặc b = c
=> Tam giác đã cho là tam giác cân có 1 góc bằng 60° nên là tam giác đều.
Từ giả thiết số đo một góc bằng trung bình cộng số đo hai góc còn lại, suy ra tam giác đã cho có ít nhất một góc bằng 60°.
Ví dụ: Từ 2A = B + C suy ra 3A = A + B + C = 180°. Do đó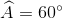
Từ 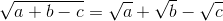(*) , suy ra tam giác đã cho là tam giác cân.
Thật vậy, bình phương các vế của (*):
a + b - c = a + b + c +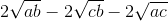
=>
=>
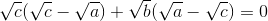
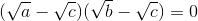
Vậy tam giác này có a = c hoặc b = c
=> Tam giác đã cho là tam giác cân có 1 góc bằng 60° nên là tam giác đều.
Câu hỏi liên quan
-
Tính giá trị biểu thức của A với x =
-
Chứng minh DM.CE=DE.CM
-
Giải phương trình (1) khi m = -5
-
Rút gọn A
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-
Cho biểu thức:
A =
Trả lời câu hỏi dưới đây:
Rút gọn A
-
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-
Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-
Giải phương trình với a = -2
-
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k