Cho tam giác ABC vuông ở A. Nửa đường tròn đường kính AB cắt BC tại D. Trên cung AD lấy một điểm E. Nối BE và kéo dài cắt AC tại F. Trả lời câu hỏi dưới đây:Gọi R, R1, R2 theo thứ tự là bán kính đường tròn ngoại tiếp các tam giác ABC, ADB, ADC. Chứng minh rằng R2 = R12 + R22

Câu hỏi
Nhận biếtCho tam giác ABC vuông ở A. Nửa đường tròn đường kính AB cắt BC tại D. Trên cung AD lấy một điểm E. Nối BE và kéo dài cắt AC tại F.
Trả lời câu hỏi dưới đây:
Gọi R, R1, R2 theo thứ tự là bán kính đường tròn ngoại tiếp các tam giác ABC, ADB, ADC. Chứng minh rằng R2 = R12 + R22
Đáp án đúng: A
Lời giải của Luyện Tập 365
Ta có: 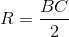 ;
; 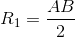 ;
; 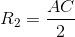 mà
mà 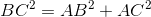
=> 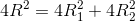
=> R2 = R12 + R22
Ta có: 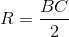 ;
; 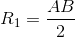 ;
; 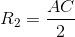 mà
mà 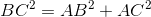
=> 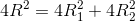
=> R2 = R12 + R22
Câu hỏi liên quan
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Chứng minh rằng: AM2 = AN.AB
-

Giải hệ phương trình

-

Tìm b để A =

-

Rút gọn biểu thức A
-

Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-

Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-

Giải phương trình (1) khi m = -5
-

Giải phương trình với a = -2
