Cho tam giác ABC và AD là đường phân giác trong. Trên đoạn thẳng AD lấy hai điểm M, N (M, N khác A và D) sao cho góc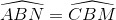 
. Đường thẳng BM cắt đường tròn ngoại tiếp tam giác ACM tại điểm thứ hai là E. Đường thẳng CN cắt đường tròn ngoại tiếp tam giác ABN tại điểm thứ hai là F. Chứng minh ba điểm A, E, F thẳng hàng.
Câu hỏi
Nhận biếtCho tam giác ABC và AD là đường phân giác trong. Trên đoạn thẳng AD lấy hai điểm M, N (M, N khác A và D) sao cho góc 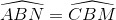. Đường thẳng BM cắt đường tròn ngoại tiếp tam giác ACM tại điểm thứ hai là E. Đường thẳng CN cắt đường tròn ngoại tiếp tam giác ABN tại điểm thứ hai là F. Chứng minh ba điểm A, E, F thẳng hàng.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Ta có:
Vì tứ giác AFBN nội tiếp nên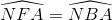 
(1)
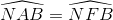(2)
Tương tự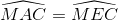 
(3)
Theo giả thiết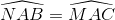 
(4)
Từ (2), (3), (4) suy ra: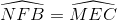 
Do đó tứ giác BCEF nội tiếp =>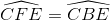 
(5)
Theo giả thiết :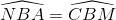 
(6)
Từ (1), (5), (6) ta có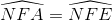 
Do đó A, E, F thẳng hàng.
Ta có:
Vì tứ giác AFBN nội tiếp nên 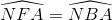(1)
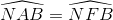(2)
Tương tự 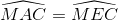(3)
Theo giả thiết 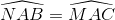(4)
Từ (2), (3), (4) suy ra: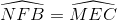
Do đó tứ giác BCEF nội tiếp => 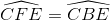(5)
Theo giả thiết : 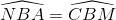(6)
Từ (1), (5), (6) ta có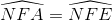
Do đó A, E, F thẳng hàng.
Câu hỏi liên quan
-
Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-
Rút gọn A
-
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Giải hệ phương trình
-
Cho biểu thức A = (
- 
+ 
) : ( x - 2 + 
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-
Rút gọn biểu thức A
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Tính giá trị biểu thức của A với x =
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-
Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a