Cho tam giác ABC có các đỉnh nằm trên đường tròn (O),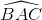 
= 45o, điểm C nằm trên cung AB lớn. Người ta kẻ dây BM vuông góc với AC và dây CN vuông góc với AB. Gọi P, Q lần lượt là các giao điểm của các cặp đường thẳng BM và CN, BN và CM. Trả lời câu hỏi dưới đây:Hãy xét vị trí tương đối của hai đường thẳng AO và PQ.
Câu hỏi
Nhận biếtCho tam giác ABC có các đỉnh nằm trên đường tròn (O), 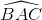= 45o, điểm C nằm trên cung AB lớn. Người ta kẻ dây BM vuông góc với AC và dây CN vuông góc với AB. Gọi P, Q lần lượt là các giao điểm của các cặp đường thẳng BM và CN, BN và CM.
Trả lời câu hỏi dưới đây:
Hãy xét vị trí tương đối của hai đường thẳng AO và PQ.
Đáp án đúng: C
Lời giải của Luyện Tập 365
TA có PC ⊥ MQ; QB ⊥ MP (chứng minh trên) nên giao điểm N của PC với QB là trực tâm của tam giác MPQ. Suy ra MN ⊥ PQ.
Mà ta lại có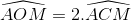 
= 2 . 45o = 90o(góc ở tâm và góc nội tiếp cùng chắn cung AM), hay AO ⊥ MN.
Vậy AO // PQ (vì cùng vuông góc với MN);
(trường hợp ∆ ABC cân đỉnh A thì OA = PQ).
TA có PC ⊥ MQ; QB ⊥ MP (chứng minh trên) nên giao điểm N của PC với QB là trực tâm của tam giác MPQ. Suy ra MN ⊥ PQ.
Mà ta lại có 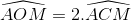= 2 . 45o = 90o(góc ở tâm và góc nội tiếp cùng chắn cung AM), hay AO ⊥ MN.
Vậy AO // PQ (vì cùng vuông góc với MN);
(trường hợp ∆ ABC cân đỉnh A thì OA = PQ).
Câu hỏi liên quan
-
Tính AC và BD biết
= 
. Chứng tỏ tích AC.BD không phụ thuộc vào -
Giải phương trình với a = -2
-
Chứng minh DM.CE=DE.CM
-
Giải hệ phương trình
-
Giải phương trình (1) khi m = -5
-
Cho biểu thức A = (
- 
+ 
) : ( x - 2 + 
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-
Cho hệ phương trình:
Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Tìm b để A =
-
Giải hệ phương trình với a = 2