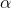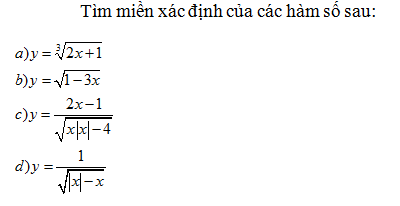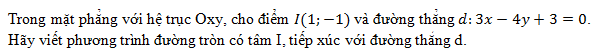Cho phương trình: 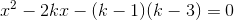 .
Chứng minh rằng với mọi k, phương trình luôn có hai nghiệm phân biệt
.
Chứng minh rằng với mọi k, phương trình luôn có hai nghiệm phân biệt 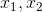 thỏa mãn:
thỏa mãn:
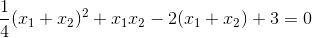 .
.

Câu hỏi
Nhận biếtCho phương trình: 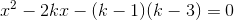 .
.
Chứng minh rằng với mọi k, phương trình luôn có hai nghiệm phân biệt 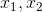 thỏa mãn:
thỏa mãn:
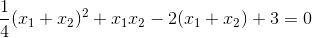 .
.
Đáp án đúng:
Lời giải của Luyện Tập 365
Ta có: 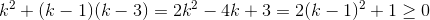 , với mọi k.
, với mọi k.
Suy ra phương trình luôn có hai nghiệm phân biệt 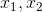 thỏa mãn:
thỏa mãn:
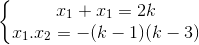
Khi đó: 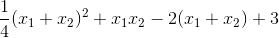
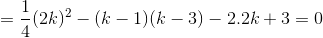 , đpcm.
, đpcm.
Ta có: 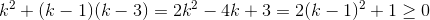 , với mọi k.
, với mọi k.
Suy ra phương trình luôn có hai nghiệm phân biệt 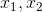 thỏa mãn:
thỏa mãn:
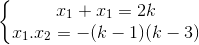
Khi đó: 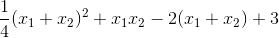
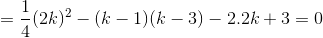 , đpcm.
, đpcm.
Câu hỏi liên quan
-

-

cơ bản

-

Xác định hàm số bậc hai
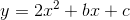 biết rằng đồ thị của nó có hoành độ đỉnh là 2 và đị qua điểm M(1;-2)
biết rằng đồ thị của nó có hoành độ đỉnh là 2 và đị qua điểm M(1;-2) -

Dùng định nghĩa để tìm khảng tăng giảm của hàm số
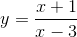
-

Dùng định nghĩa để xác định khoảng tăng giảm của hàm số sau:
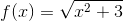
-

Dùng định nghĩa tìm khoảng tăng giảm của hàm số:
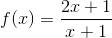
-

-

Tìm tập xác định của các hàm số sau:
a)
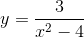
b)
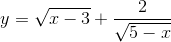
c)
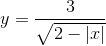
-

Dùng định nghĩa tính khoảng tăng giảm của hàm số:
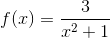
-

Cho góc
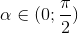 thỏa mãn
thỏa mãn 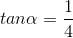 .. Tính các giá trị lượng giác còn lại của
.. Tính các giá trị lượng giác còn lại của