Cho nửa đường tròn tâm O, đường kính AB và một điểm M nằm trên nửa đường tròn đó. Người ta kẻ trên nửa mặt phẳng, bờ AB, có chứa điểm M các tia Ax, By vuông góc với AB. Một đường tròn (O’) đi qua A, M cắt đoạn thẳng AB và tia Ax lần lượt tại các điểm C, P ; đường thẳng PM cắt By tại một điểm Q. Trả lời câu hỏi dưới đây:Nêu nhận xét và giải thích về vị trí tương đối của đường thẳng QC và đường tròn (O’).
Câu hỏi
Nhận biếtCho nửa đường tròn tâm O, đường kính AB và một điểm M nằm trên nửa đường tròn đó. Người ta kẻ trên nửa mặt phẳng, bờ AB, có chứa điểm M các tia Ax, By vuông góc với AB. Một đường tròn (O’) đi qua A, M cắt đoạn thẳng AB và tia Ax lần lượt tại các điểm C, P ; đường thẳng PM cắt By tại một điểm Q.
Trả lời câu hỏi dưới đây:
Nêu nhận xét và giải thích về vị trí tương đối của đường thẳng QC và đường tròn (O’).
Đáp án đúng: A
Lời giải của Luyện Tập 365
Vì trong (O'), PC là đường kính (do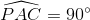 
) và 
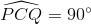theo bài 2 nên QC là tiếp tuyến của (O') (định lí).
Vì trong (O'), PC là đường kính (do 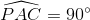) và 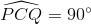theo bài 2 nên QC là tiếp tuyến của (O') (định lí).
Câu hỏi liên quan
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-
Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-
Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-
Tìm a để phương trình có 2 nghiệm nguyên
-
Giải hệ phương trình
-
Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-
Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-
Giải phương trình (1) khi m = -5
-
Giải hệ phương trình với a = 2