Cho một hình chữ nhật ABCD, AB = b, BC =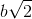 
. Từ A kẻ đường thẳng vuông góc với BD cắt BC và BD theo thứ tự tại M và N. Trả lời câu hỏi dưới đây:Chứng minh rằng M là trung điểm của BC.
Câu hỏi
Nhận biếtCho một hình chữ nhật ABCD, AB = b, BC = . Từ A kẻ đường thẳng vuông góc với BD cắt BC và BD theo thứ tự tại M và N.
Trả lời câu hỏi dưới đây:
Chứng minh rằng M là trung điểm của BC.
Đáp án đúng: A
Lời giải của Luyện Tập 365
∆ BNM ~ ∆ BCD (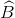
chung) =>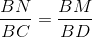 
=> 
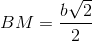
=> M là trung điểm của BC.
∆ BNM ~ ∆ BCD ( chung) =>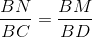
=>
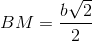
=> M là trung điểm của BC.
Câu hỏi liên quan
-
Tính AC và BD biết
= 
. Chứng tỏ tích AC.BD không phụ thuộc vào -
Chứng minh rằng: AM2 = AN.AB
-
Chứng minh DM.CE=DE.CM
-
Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-
Giải hệ phương trình
-
Giải phương trình (1) khi m = -5
-
Giải hệ phương trình với a = 2
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2