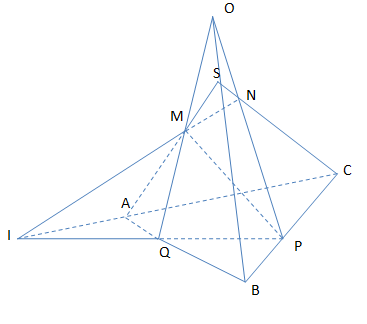
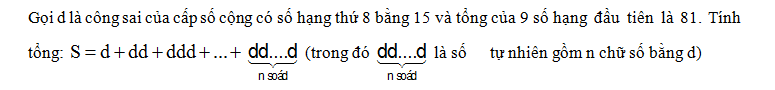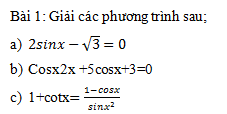Cho M ; N ; P là 3 điểm tùy ý trên các cạnh SA ; SC ; BC của tứ diện SABC. a) Tìm giao điểm Q của (MNP) với cạnh AB b) Chứng minh QM ; SB , PN đồng qui
Câu hỏi
Nhận biếtCho M ; N ; P là 3 điểm tùy ý trên các cạnh SA ; SC ; BC của tứ diện SABC.
a) Tìm giao điểm Q của (MNP) với cạnh AB
b) Chứng minh QM ; SB , PN đồng qui
Đáp án đúng:
Lời giải của Luyện Tập 365
a) Trong mặt phẳng (SAC) ta có :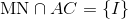 
Trong mặt phẳng (ABC) ta có :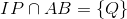 
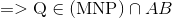
b) Trong mặt phẳng (INP) ta có: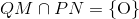 
Do 3 điểm S ; B ; O thuộc giao tuyến của 2 mặt phẳng (AQM) và (CPN) nên S ;B ; O thẳng hàng
=> Điều phải chứng minh
a) Trong mặt phẳng (SAC) ta có :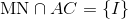
Trong mặt phẳng (ABC) ta có :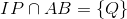
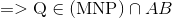
b) Trong mặt phẳng (INP) ta có: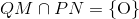
Do 3 điểm S ; B ; O thuộc giao tuyến của 2 mặt phẳng (AQM) và (CPN) nên S ;B ; O thẳng hàng
=> Điều phải chứng minh
Câu hỏi liên quan
-
-
-
Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?
-
Giải các phương trình sau:
a)
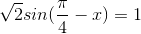
b)
-
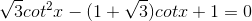
bai 3 de 2 HK1 minh khai ha tinh 13-14
-
Giải các phương trình sau:
a)
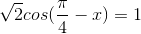
b)
-
-
-
-
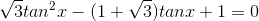
Cho
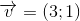và đường thẳng d: y=2x+4. Tìm ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 
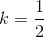và phép tịnh tiến theo vecto 
.
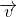