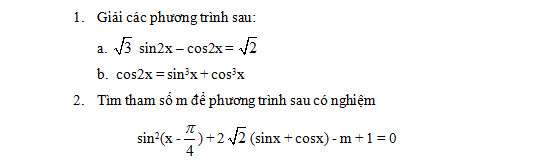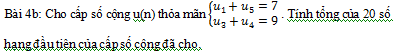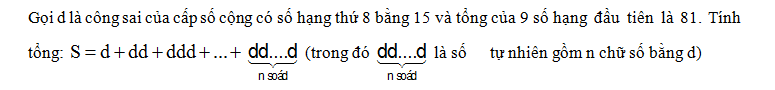Cho hình thang ABCD có AB // CD và S không thuộc mặt phẳng (ABCD) . Trên SA ; BD lấy 2 điểm M , N sao cho 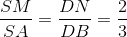 . Kẻ NI // AB ( I
. Kẻ NI // AB ( I  AD) .
a) Chứng minh : MI // (SBD) ; (MNI) // (SCD) . Suy ra MN // (SCD)
b) Tìm P
AD) .
a) Chứng minh : MI // (SBD) ; (MNI) // (SCD) . Suy ra MN // (SCD)
b) Tìm P 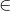 (MNI)
(MNI)  SB . Chứng minh PJ // SC
SB . Chứng minh PJ // SC

Câu hỏi
Nhận biếtCho hình thang ABCD có AB // CD và S không thuộc mặt phẳng (ABCD) . Trên SA ; BD lấy 2 điểm M , N sao cho 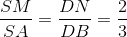 . Kẻ NI // AB ( I
. Kẻ NI // AB ( I  AD) .
AD) .
a) Chứng minh : MI // (SBD) ; (MNI) // (SCD) . Suy ra MN // (SCD)
b) Tìm P 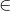 (MNI)
(MNI)  SB . Chứng minh PJ // SC
SB . Chứng minh PJ // SC
Đáp án đúng:
Lời giải của Luyện Tập 365
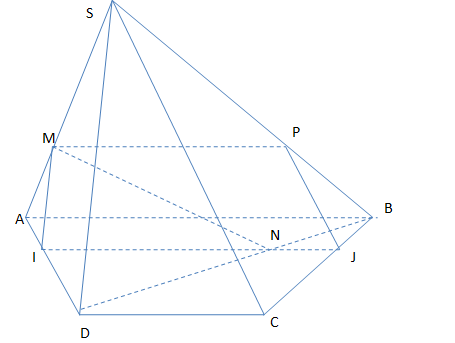
a) Ta có : 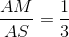
Do NI // AB nên 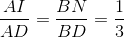
Suy ra : 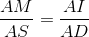
=> MI // SD => MI // (SBD)
Do NI // AB => NI // CD
Vậy (MNI) // (SCD) nên MN // (SCD)
b) Trong mặt phẳng (ABCD) ta có : NI  BC = {J}
BC = {J}
Do AB // IJ suy ra (SAB) cắt (IMN) theo giao tuyến MP và MP // AB // IJ
Vậy P 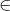 SB
SB  (MNI)
(MNI)
Ta có : MP // AB do đó : 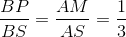
IJ // AB do đó : 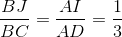
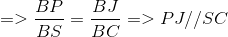

a) Ta có : 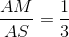
Do NI // AB nên 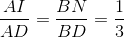
Suy ra : 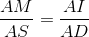
=> MI // SD => MI // (SBD)
Do NI // AB => NI // CD
Vậy (MNI) // (SCD) nên MN // (SCD)
b) Trong mặt phẳng (ABCD) ta có : NI  BC = {J}
BC = {J}
Do AB // IJ suy ra (SAB) cắt (IMN) theo giao tuyến MP và MP // AB // IJ
Vậy P 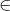 SB
SB  (MNI)
(MNI)
Ta có : MP // AB do đó : 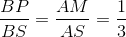
IJ // AB do đó : 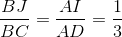
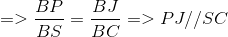
Câu hỏi liên quan
-

Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 8.
b) Tích số chấm hai mặt xuất hiện là số lẻ.
-

-


bai 3 de 2 HK1 minh khai ha tinh 13-14
-

Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?
-

-

-

: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn).
a) Xác định giao tuyến của hai cặp mặt phẳng (SAC) và (SBD) ;(SAD) và (SBC).
b) M là một điểm trên cạnh SC không trùng với S và C. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (ABM).
c) Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC), chứng minh d và BM đồng phẳng.
-

-

-