Cho hình bình hành ABCD và n = 4k + 1 ( k nguyên dương) đường thẳng. Mỗi đường thẳng đó chia hình bình hành ABCD thành 2 hình thang có tỉ số diện tích là m ( m là số nguyên dương cho trước). Chứng minh rằng có ít nhất k + 1 đường thẳng trong số n đường thẳng nói trên đồng quy. ( Hình bình hành cũng được xem như hình thang).
Câu hỏi
Nhận biếtCho hình bình hành ABCD và n = 4k + 1 ( k nguyên dương) đường thẳng. Mỗi đường thẳng đó chia hình bình hành ABCD thành 2 hình thang có tỉ số diện tích là m ( m là số nguyên dương cho trước). Chứng minh rằng có ít nhất k + 1 đường thẳng trong số n đường thẳng nói trên đồng quy. ( Hình bình hành cũng được xem như hình thang).
Đáp án đúng: A
Lời giải của Luyện Tập 365
Gọi d là đường thẳng bất kì trong số n đường thẳng đã cho. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB, AD , DC, CB . Giả sử d cắt AB tại E, d cắt DC tại F. Gọi I là giao điểm của d và NQ, h là khoảng cách giữa hai đường thẳng AB và CD.
Ta có: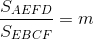 
<=> 
.
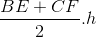
<=> NI = m.IQ <=>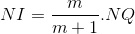 
,suy ra điểm cố định
Tương tự ta tìm được ba điểm J,K,L cố định mà các đường thẳng đẫ cho đi qua chúng. Theo nguyên lí Dirichle tồn tại một điểm mà có ít nhất k + 1 đường thẳng đi qua.
Gọi d là đường thẳng bất kì trong số n đường thẳng đã cho. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB, AD , DC, CB . Giả sử d cắt AB tại E, d cắt DC tại F. Gọi I là giao điểm của d và NQ, h là khoảng cách giữa hai đường thẳng AB và CD.
Ta có: <=> .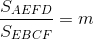
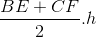
<=> NI = m.IQ <=> 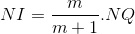,suy ra điểm cố định
Tương tự ta tìm được ba điểm J,K,L cố định mà các đường thẳng đẫ cho đi qua chúng. Theo nguyên lí Dirichle tồn tại một điểm mà có ít nhất k + 1 đường thẳng đi qua.
Câu hỏi liên quan
-
Cho biểu thức A = (
- 
+ 
) : ( x - 2 + 
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-
Tìm m để phương trình (1) có nghiệm .
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Cho biểu thức:
A =
Trả lời câu hỏi dưới đây:
Rút gọn A
-
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Giải hệ phương trình với a = 2
-
Chứng minh rằng: AM2 = AN.AB
-
Tìm a để phương trình có 2 nghiệm nguyên
-
Chứng minh DM.CE=DE.CM