Cho hai đường tròn (O) và (O') bán kính khác nhau, cắt nhau tại A và B (O và O' thuộc hai nửa mặt phẳng bờ AB). Qua A vẽ hai cát tuyến CAD, EAF (C và E thuộc (O), D và F thuộc (O'), E thuộc cung AC). Trả lời câu hỏi dưới đây:EC và DF cắt nhau ở P. Chứng minh tứ giác EPFB nội tiếp được đường tròn.

Câu hỏi
Nhận biếtCho hai đường tròn (O) và (O') bán kính khác nhau, cắt nhau tại A và B (O và O' thuộc hai nửa mặt phẳng bờ AB). Qua A vẽ hai cát tuyến CAD, EAF (C và E thuộc (O), D và F thuộc (O'), E thuộc cung AC).
Trả lời câu hỏi dưới đây:
EC và DF cắt nhau ở P. Chứng minh tứ giác EPFB nội tiếp được đường tròn.
Đáp án đúng: A
Lời giải của Luyện Tập 365

Ta có:
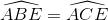 (hai góc nội tiếp chắn cung AE của đường tròn (O)).
(hai góc nội tiếp chắn cung AE của đường tròn (O)).
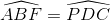 (cùng bù với góc ADF)
(cùng bù với góc ADF)
=> 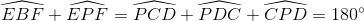
Tứ giác PEBF nội tiếp được.

Ta có:
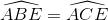 (hai góc nội tiếp chắn cung AE của đường tròn (O)).
(hai góc nội tiếp chắn cung AE của đường tròn (O)).
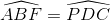 (cùng bù với góc ADF)
(cùng bù với góc ADF)
=> 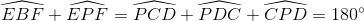
Tứ giác PEBF nội tiếp được.
Câu hỏi liên quan
-

Tính giá trị biểu thức của A với x =

-

Giải hệ phương trình với a = 2
-

Cho biểu thức A = (
 -
-  +
+  ) : ( x - 2 +
) : ( x - 2 +  )
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-

Chứng minh rằng: AM2 = AN.AB
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-

Rút gọn biểu thức A
-

Tìm b để A =

-

Giải phương trình (1) khi m = -5
