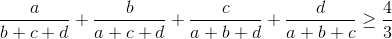Cho góc 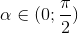 thỏa mãn
thỏa mãn 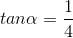 .. Tính các giá trị lượng giác còn lại của
.. Tính các giá trị lượng giác còn lại của 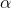

Câu hỏi
Nhận biết Cho góc 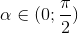 thỏa mãn
thỏa mãn 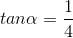 .. Tính các giá trị lượng giác còn lại của
.. Tính các giá trị lượng giác còn lại của 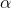
Đáp án đúng:
Lời giải của Luyện Tập 365
Áp dụng công thức 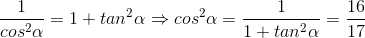
Vì 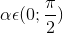 nên
nên 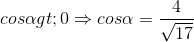
Lại có 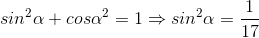
Và 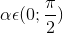 nên
nên 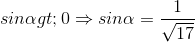
Và 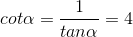
Áp dụng công thức 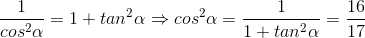
Vì 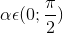 nên
nên 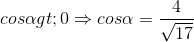
Lại có 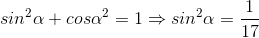
Và 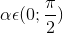 nên
nên 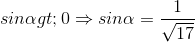
Và 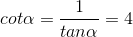
Câu hỏi liên quan
-

Dùng định nghĩa để xác định khoảng tăng giảm của hàm số sau:
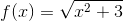
-

Tìm miền xác định của hàm số sau:

-

Phần nâng cao
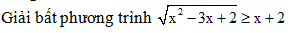

-

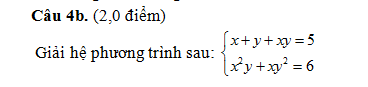
Giải và biện luận phương trình sau theo tham số m
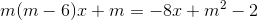
-

Phần nâng cao

-

cơ bản

-

Cho tam giác ABC với A(-1;3);B(2;5);C(0;-3).
a) Tính tọa độ trọng tâm G của tam giác ABC.
b) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành
-

Phần cơ bản
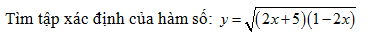

-

BAN NÂNG CAO
-

Cho a, b, c, d là các số thực dương. Chứng minh rằng: