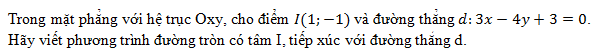Cho điểm A(1; -1) và B(3;0) là hai đỉnh của hình vuông ABCD. Tìm toạ độ các đỉnh C và D.

Câu hỏi
Nhận biếtCho điểm A(1; -1) và B(3;0) là hai đỉnh của hình vuông ABCD. Tìm toạ độ các đỉnh C và D.
C\left( {4;\,\,2} \right),\,\,D\left( {2; - 3} \right)\\
C\left( {2;\,\, - 2} \right),\,\,D\left( {0;\,\,1} \right)
\end{array} \right.\)
C\left( {4; - 2} \right),\,\,D\left( {2; - 3} \right)\\
C\left( {2;\,\,2} \right),\,\,D\left( {0;\,\,1} \right)
\end{array} \right.\)
Đáp án đúng: D
Lời giải của Luyện Tập 365
Gọi \(C\left( {x;\,\,y} \right).\) Khi đó \(\overrightarrow {AB} (2;1);{\rm{ }}\overrightarrow {BC} \left( {x - 3;y} \right)\) .
Từ ABCD là hình vuông, ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}\overrightarrow {AB} \bot \overrightarrow {BC} \\AB = BC\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2(x - 3) + 1.y = 0\\{(x - 3)^2} + {y^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 6 + y = 0\\{(x - 3)^2} + {y^2} = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 6 - 2x\\{x^2} - 6x + 9 + 36 - 24x + 4{x^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 6 - 2x\\5{x^2} - 30x + 40 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 4\\y = - 2\end{array} \right.\\\left\{ \begin{array}{l}x = 2\\y = 2\end{array} \right.\end{array} \right.\end{array}\)
Với C(4;-2) ta có \(\overrightarrow {DC} = \overrightarrow {AB} \Rightarrow \left\{ \begin{array}{l}4 - {x_D} = 2\\ - 2 - {y_D} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_D} = 2\\{y_D} = - 3\end{array} \right. \Rightarrow D(2; - 3)\)
Với C(2;2) ta có \(\overrightarrow {DC} = \overrightarrow {AB} \Rightarrow \left\{ \begin{array}{l}2 - {x_D} = 2\\2 - {y_D} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_D} = 0\\{y_D} = 1\end{array} \right. \Rightarrow D(0;1)\)
Gọi \(C\left( {x;\,\,y} \right).\) Khi đó \(\overrightarrow {AB} (2;1);{\rm{ }}\overrightarrow {BC} \left( {x - 3;y} \right)\) .
Từ ABCD là hình vuông, ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}\overrightarrow {AB} \bot \overrightarrow {BC} \\AB = BC\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2(x - 3) + 1.y = 0\\{(x - 3)^2} + {y^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 6 + y = 0\\{(x - 3)^2} + {y^2} = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 6 - 2x\\{x^2} - 6x + 9 + 36 - 24x + 4{x^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 6 - 2x\\5{x^2} - 30x + 40 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 4\\y = - 2\end{array} \right.\\\left\{ \begin{array}{l}x = 2\\y = 2\end{array} \right.\end{array} \right.\end{array}\)
Với C(4;-2) ta có \(\overrightarrow {DC} = \overrightarrow {AB} \Rightarrow \left\{ \begin{array}{l}4 - {x_D} = 2\\ - 2 - {y_D} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_D} = 2\\{y_D} = - 3\end{array} \right. \Rightarrow D(2; - 3)\)
Với C(2;2) ta có \(\overrightarrow {DC} = \overrightarrow {AB} \Rightarrow \left\{ \begin{array}{l}2 - {x_D} = 2\\2 - {y_D} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_D} = 0\\{y_D} = 1\end{array} \right. \Rightarrow D(0;1)\)
Câu hỏi liên quan
-

Dùng định nghĩa tính khoảng tăng giảm của hàm số:
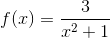
-

Phần nâng cao

-

-

Tìm tập xác định của hàm số sau;
a)
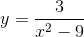
b)
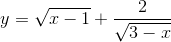
c)
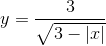
-

BAN NÂNG CAO

-

Dùng định nghĩa để xác định khoảng tăng giảm của hàm số sau:
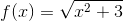
-

Phần cơ bản
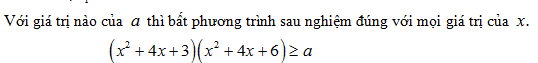
-

Cho a, b, c, d là các số thực dương. Chứng minh rằng:
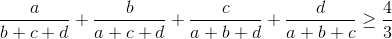
-

Tìm tập xác định của các hàm số sau:
a)
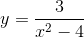
b)
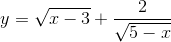
c)
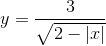
-

Cho tam giác ABC với A(-1;3);B(2;5);C(0;-3).
a) Tính tọa độ trọng tâm G của tam giác ABC.
b) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành