Cho biểu thức 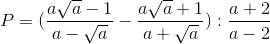$P=(\frac{a\sqrt{a}-1}{a-\sqrt{a}}-\frac{a\sqrt{a}+1}{a+\sqrt{a}}):\frac{a+2}{a-2}$ với a > 0, a ≠ 1, a ≠ 2. Trả lời câu hỏi dưới đây:Rút gọn P

Nhận biết

Cho biểu thức 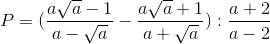$P=(\frac{a\sqrt{a}-1}{a-\sqrt{a}}-\frac{a\sqrt{a}+1}{a+\sqrt{a}}):\frac{a+2}{a-2}$ với a > 0, a ≠ 1, a ≠ 2.

Trả lời câu hỏi dưới đây:

Rút gọn P

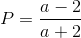
$P=\frac{a-2}{a+2}$

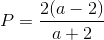
$P=\frac{2(a-2)}{a+2}$

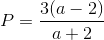
$P=\frac{3(a-2)}{a+2}$

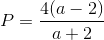
$P=\frac{4(a-2)}{a+2}$

Giải hệ phương trình với a = 2

Chi tiết
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.

Chi tiết
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k

Chi tiết
Chứng minh DM.CE=DE.CM

Chi tiết
Cho biểu thức A = ( $frac{x^{2}}{x^{3}-4x}$ - $frac{6}{3x-6}$ + $frac{1}{x+2}$ ) : ( x - 2 + $frac{10-x^{2}}{x+2}$ )

Trả lời câu hỏi dưới đây:

Rút gọn biểu thức A

Chi tiết
Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x₁ và x₂. Chứng minh rằng: x₁x₂=-1, từ đó suy ra tam giác MON là tam giác vuông

Chi tiết
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K

Chi tiết
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm

Chi tiết
Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.

Trả lời câu hỏi dưới đây:

Chứng minh rằng: AM² = AN.AB

Chi tiết
Tìm m để phương trình (1) có nghiệm .

Chi tiết

Cho biểu thức với a > 0, a ≠ 1, a ≠ 2. Trả lời câu hỏi dưới đây:Rút gọn P