Cho a ≥ 1, b ≥ 1. Chứng minh rằng 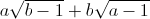

Câu hỏi
Nhận biếtCho a ≥ 1, b ≥ 1. Chứng minh rằng 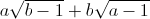
A.
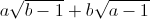 =
= 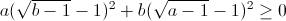 với a ≥ 1, b ≥ 1.
với a ≥ 1, b ≥ 1.
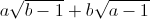 =
= 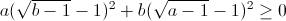 với a ≥ 1, b ≥ 1.
với a ≥ 1, b ≥ 1.
B.
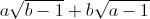 =
= 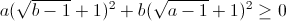 với a ≥ 1, b ≥ 1.
với a ≥ 1, b ≥ 1.
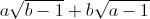 =
= 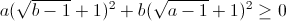 với a ≥ 1, b ≥ 1.
với a ≥ 1, b ≥ 1.
C.
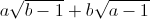 =
= 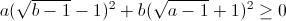 với a ≥ 1, b ≥ 1.
với a ≥ 1, b ≥ 1.
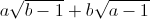 =
= 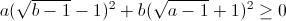 với a ≥ 1, b ≥ 1.
với a ≥ 1, b ≥ 1.
D.
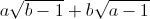 =
= 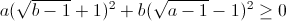 với a ≥ 1, b ≥ 1.
với a ≥ 1, b ≥ 1.
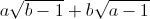 =
= 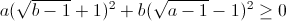 với a ≥ 1, b ≥ 1.
với a ≥ 1, b ≥ 1. Đáp án đúng: A
Lời giải của Luyện Tập 365
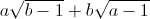 <=>
<=> 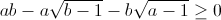
<=> 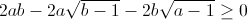
<=> ![[a(b-1)-2a\sqrt{b-1}+a]+[b(a-1)-2b\sqrt{a-1}+b]\geq 0](https://luyentap365.com/wp-content/picture/learning/exam/2014/0124/v18840_255525_4.gif)
<=> 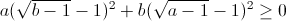
(Bất đẳng thức đúng với mọi a ≥ 1, b ≥ 1)
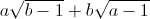 <=>
<=> 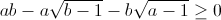
<=> 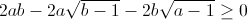
<=> ![[a(b-1)-2a\sqrt{b-1}+a]+[b(a-1)-2b\sqrt{a-1}+b]\geq 0](https://luyentap365.com/wp-content/picture/learning/exam/2014/0124/v18840_255525_4.gif)
<=> 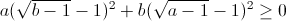
(Bất đẳng thức đúng với mọi a ≥ 1, b ≥ 1)
Câu hỏi liên quan
-

Giải phương trình (1) khi m = -5
-

Giải hệ phương trình với a = 2
-

Chứng minh DM.CE=DE.CM
-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Giải phương trình với a = -2
-

Tìm m để phương trình (1) có nghiệm .
-

Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-

Giải hệ phương trình

-

Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-

Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
