Skip to main content
/ Luyện Thi Vào Lớp 10 Môn Toán / Câu hỏi 54356

Cho 5 điểm xếp thẳng hàng theo thứ tự A, B, C, D, E và AB = BC = CD = DE = a. Dây MN của đường tròn (C; AC) vuông góc với AD tại D; AM cắt đường tròn (B; AB) tại K. Trả lời câu hỏi dưới đây:Tìm diện tích hình giới hạn bởi ba đường tròn (C; AC); (B; AB) và đường tròn ngoại tiếp tứ giác KMDC.

Cho 5 điểm xếp thẳng hàng theo thứ tự A, B, C, D, E và AB = BC = CD = DE = a. Dây MN của

Câu hỏi

Nhận biết

Cho 5 điểm xếp thẳng hàng theo thứ tự A, B, C, D, E và AB = BC = CD = DE = a. Dây MN của đường tròn (C; AC) vuông góc với AD tại D; AM cắt đường tròn (B; AB) tại K.

Trả lời câu hỏi dưới đây:

Tìm diện tích hình giới hạn bởi ba đường tròn (C; AC); (B; AB) và đường tròn ngoại tiếp tứ giác KMDC.


A.
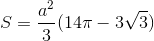
S=\frac{a^{2}}{3}(14\pi -3\sqrt{3})
B.
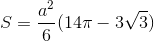
S=\frac{a^{2}}{6}(14\pi -3\sqrt{3})
C.
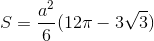
S=\frac{a^{2}}{6}(12\pi -3\sqrt{3})
D.
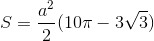
S=\frac{a^{2}}{2}(10\pi -3\sqrt{3})
Đáp án đúng: B

Lời giải của Luyện Tập 365

Gọi diện tích phải tìm là S (phần gạch sọc) bằng diện tích hình tròn cộng với hai diện tích viên phân trừ đi diện tích hai hình tròn (B; a).

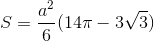
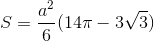
Ta có: S=\frac{a^{2}}{6}(14\pi -3\sqrt{3})

Câu hỏi liên quan

  • Rút gọn A

    Rút gọn A

    Chi tiết
  • Cho Parabol  (P): ax2(a ≠ 0) và đường thẳng d: y=2x

    Cho Parabol  (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.

    Chi tiết
  • Tính AC và BD biết

    Tính AC và BD biết widehat{AOC} = alpha. Chứng tỏ tích AC.BD không phụ thuộc vào  alpha

    Chi tiết
  • Cho hệ phương trình:

    Cho hệ phương trình: left{begin{matrix} x + ay = 3a\ ax - y = a^{2}-2 end{matrix}right.

    Trả lời câu hỏi dưới đây:

    Giải hệ phương trình với a = 2

    Chi tiết
  • Cho phương trình: ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)

    Cho phương trình: 

    ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)

    Trả lời câu hỏi dưới đây:

    Giải phương trình với a = -2

    Chi tiết
  • Rút gọn biểu thức A

    Rút gọn biểu thức A

    Chi tiết
  • Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm

    Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm

    Chi tiết
  • Tìm b để A =

    Tìm b để A = frac{5}{2}

    Chi tiết
  • Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2.

    Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1  và x2. Chứng minh rằng:  x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông

    Chi tiết
  • Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đư

    Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.

    Trả lời câu hỏi dưới đây:

    Chứng minh rằng: AM2 = AN.AB

    Chi tiết