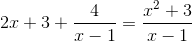Môn Toán Lớp 10
Bất Đẳng Thức - Bất Phương Trình
-
Tìm nghiệm của bất phương trình:\(\left( {2x - 2} \right)\sqrt {2x - 1} \le 6\left( {x - 1} \right)\)
-
Giải bất phương trình \(\sqrt {{x^2} - 3x + 2} + \sqrt {{x^2} - 4x + 3} \ge 2\sqrt {{x^2} - 5x + 4} \) .
-
Hệ bất phương trình \(\left\{ \begin{array}{l}{x^2} - 4x + 3 > 0\\3{x^2} - 10x + 3 \le 0\\4{x^2} - x - 3 > 0\end{array} \right.\) có nghiệm là:
Phương Pháp Tọa Độ Trong Mặt Phẳng
-
. Cho tam giác ABC với A(-1;2);B(-2;5);C(0;-3).
a) Tính tọa độ trọng tâm G của tam giác ABC.
b) Tìm tọa độ điểm D sao cho tứ giác ADBC là hình bình hành
-
Cho tam giác ABC với A(-1;3);B(2;5);C(0;-3).
a) Tính tọa độ trọng tâm G của tam giác ABC.
b) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành
Tích vô hướng của hai vec tơ và ứng dụng
-
Cho điểm A(1; -1) và B(3;0) là hai đỉnh của hình vuông ABCD. Tìm toạ độ các đỉnh C và D.
-
Cho \(\Delta ABC\) có \(AB = 2,\,\,AC = 3\) và \(\angle A = {120^0}.\) \(M\) là trung điểm của \(BC.\)
a) Tính \(BC.\)
b) Tính \(AM.\)
-
Cho hai điểm A(-3;2), B(4;3). Điểm N nằm trên trục Oy sao cho NA=NB. Khi đó N có toạ độ:
Vec tơ
-
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(6;3),B(-3;6),C(1;-2).
a) Chứng minh A,B,C là ba đỉnh một tam giác.
b) Xác định điểm D trên trục hoành sao cho ba điểm A,B,D thẳng hàng.
c) Xác định điểm E trên cạnh BC sao cho BE=2EC.
d) Xác định giao điểm hai đường thẳng DE và AC
-
Trong mặt phẳng tọa độ Oxy cho A(3;-1),B(-1;2) và I(1;-1). Xác định tọa độ C,D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa độ tâm O của hình bình hành ABCD.
-
Cho tam giác ABC có A(3;4),B(2;1),C(-1;-2). Tìm điểm M trên đường thẳng BC sao cho SABC=3SABM

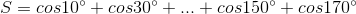
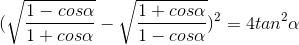
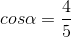
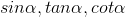 .
.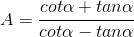
 .
. .
.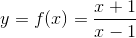 .
.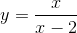 .
.