Luyện Thi Vào Lớp 10 Môn Toán
+ 
+ 
= 
Đường Tròn
-
Cho đường tròn tâm O đường kính AB = 2R. Gọi M là một điểm bất kì thuộc đường tròn (O) khác A và B. Các tiếp tuyến của (O) tại A và M cắt nhau tại E. Vẽ MP vuông góc với AB (P thuộc AB). Vẽ MQ vuông góc với AE (Q thuộc AE).
Trả lời câu hỏi dưới đây:
Đặt AP = x. Tính MP theo R và x. Tìm vị trí của M trên (O) để hình chữ nhật APMQ có diện tích lớn nhật.
-
Cho đường tròn tâm O đường kính AB = 2R. Gọi M là một điểm bất kì thuộc đường tròn (O) khác A và B. Các tiếp tuyến của (O) tại A và M cắt nhau tại E. Vẽ MP vuông góc với AB (P thuộc AB). Vẽ MQ vuông góc với AE (Q thuộc AE).
Trả lời câu hỏi dưới đây:
Gọi K là giao điểm của PQ. Chứng minh hai tam giác EAO và MPB đồng dạng. Suy ra K là trung điểm của MP.
-
Cho đường tròn tâm O đường kính AB = 2R. Gọi M là một điểm bất kì thuộc đường tròn (O) khác A và B. Các tiếp tuyến của (O) tại A và M cắt nhau tại E. Vẽ MP vuông góc với AB (P thuộc AB). Vẽ MQ vuông góc với AE (Q thuộc AE).
Trả lời câu hỏi dưới đây:
Gọi I là trung điểm của PQ. Chứng minh O, I, E thẳng hàng.
Góc Với Đường Tròn
-
Cho tam giác ABC có 3 góc nhọn nội tiếp trong đường tròn tâm O. Kẻ các đường cao BB’ và CC’ (b’ thuộc cạnh AC, C’ thuộc cạnh AB). Đường thẳng B’C’ cắt đường tròn tâm O tại hai điểm là M và N (theo thứ tự N, C’,B’, M).
Trả lời câu hỏi dưới đây:
AM2 = AC’.AB.
-
Cho tam giác ABC có 3 góc nhọn nội tiếp trong đường tròn tâm O. Kẻ các đường cao BB’ và CC’ (b’ thuộc cạnh AC, C’ thuộc cạnh AB). Đường thẳng B’C’ cắt đường tròn tâm O tại hai điểm là M và N (theo thứ tự N, C’,B’, M).
Trả lời câu hỏi dưới đây:
Chứng minh AM = AN.
-
Cho tam giác ABC vuông tại A và AC > AB, D là một điểm trên cạnh AC sao cho CD < AD. Vẽ đường tròn (D) tâm D và tiếp xúc với BC tại E. Từ B vẽ tiếp tuyến thứ hai của đường tròn (D) với F là tiếp điểm khác E.
Trả lời câu hỏi dưới đây:
Chứng minh rằng tam giác ANF là tam giác cân.
Hàm Số Bậc Nhất
-
Cho a, b , c là các số nguyên sao cho 2a + b, 2b + c, 2c + a đều là các số chính phương (*).
Trả lời câu hỏi dưới đây:
Tồn tại hay không các số nguyên a, b, c thỏa mãn điều kiện (*) sao cho (a – b)(b – c)(c – a) không chia hết cho 27.
-
R = (
+ 
):(
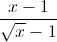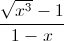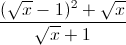) với x ≥ 0 và x ≠ 1.Trả lời câu hỏi dưới đây:
Chứng minh R < 1.
-
Cho A =
- 
- 
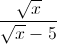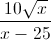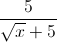, với x ≥ 0 và x ≠ 25.Trả lời câu hỏi dưới đây:
Tìm x để A <
Hàm Số y=ax2 (a ≠ 0), Phương Trình Bậc Hai Một Ẩn
-
Cho hàm số y = ax2
Trả lời câu hỏi dưới đây:
Vẽ trên cùng một mặt phẳng tọa độ đồ thị (P) của hàm số đã cho với giá trị a vừa tìm được và đường thẳng (d) đi qua M( - 2; 8) có hệ số góc bằng – 2. Tìm tọa độ giao điểm khác M của (P) và (d).
-
Cho phương trình x2 – (3m + 1)x + 2m2 + m – 1 = 0 (x là ẩn số).
Trả lời câu hỏi dưới đây:
Gọi x1, x2 là các nghiệm của phương trình . Tìm m để biểu thức sau đạt giá trị lớn nhất: A = x12 + x22 – 3x1x2.
-
Cho hàm số y = 2.x2 có đồ thị (P) và y = x + 3 có đồ thị (d).
Trả lời câu hỏi dưới đây:
Đường thẳng (∆) cắt trục tung tại C, cắt trục hoành tại D. Đường thẳng (d) cắt trục hoành tại B. Tính tỉ số diện tích của hai tam giác ABC và tam giác ABD.
Hệ Hai Phương Trình Bậc Nhất Hai Ẩn
-
Giải:
Trả lời câu hỏi dưới đây:
Tìm các số nguyên m để hệ phương trình
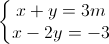có nghiệm (x;y) thỏa mãn điều kiện x2 + xy = 30 -
Giải phương trình và hệ phương trình sau:
Giải hệ phương trình:
-
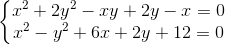
Cho hệ phương trình:
Trả lời câu hỏi dưới đây:
Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
Hệ Thức Lượng Trong Tam Giác Vuông
-
Cho tam giác ABC vuông tại A, kẻ đường cao AH và phân giác BE của góc ABC ( H thuộc BC, E thuộc AC), kẻ AD vuông góc với BE ( D thuộc BE).
Trả lời câu hỏi dưới đây:
Cho biết
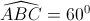và AB = a (a>0 cho trước). Tính theo a diện tích phần tam giác ABC nằm ngoài đường tròn(O) -
Cho tam giác ABC vuông tại A, kẻ đường cao AH và phân giác BE của góc ABC ( H thuộc BC, E thuộc AC), kẻ AD vuông góc với BE ( D thuộc BE).
Trả lời câu hỏi dưới đây:
chứng minh
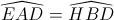và OD//HB -
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm O, đường kính AH, đường tròn này cắt các cạnh AB, AC theo thứ tự tại D và E.
Trả lời câu hỏi dưới đây:
Cho biết AB = 3cm, BC = 5 cm. Tính diện tích tứ giác BDEC.
Hình Giải Tích Phẳng
-
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
Hình Trụ - Hình Nón - Hình Cầu
-
Từ một tấm thiếc hình chữ nhật ABCD có chiều rộng AB = 3,6 dm, chiều dài AD = 4,85 dm, người ta cắt một phần tấm thiếc để làm mặt xung quanh của một hình nón với đỉnh là A và đường sinh bằng 3,6dm, sao cho diện tích mặt xung quanh này lớn nhất. Mặt đáy của hình nón được cắt trong phần còn lại của tấm thiếc hình chữ nhật ABCD.
Trả lời câu hỏi dưới đây:
Chứng tỏ rằng có thể cắt được nguyên ven hình nón đáy mà chỉ sử dụng phần còn lại của tấm thiếc ABCD sau khi đã cắt xong mặt xung quanh hình nón nói trên.
-
Cho hình nón có đường sinh là 5 cm, diện tích toàn phần là
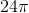cm2 .Tính thể tích hình nón. -
Một hình nón có bán kính đường tròn đáy r = 5 và thể tích V = 100π
Tính chiều cao và độ dài đường sinh
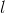của hình nón
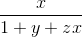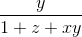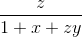