Tìm số phức z thỏa mãn : |z| = √2 và z2 là số thuần ảo.
DANH SÁCH CÂU HỎI
-
[Tìm số phức z thỏa mãn : |z| = √2 và z2 là số thuần ảo. - Luyện Tập 365]
-
[Cho số phức z thỏa mãn z2 – 2(1 + i)z + 2i = 0. Tìm phần thực và phần ảo - Luyện Tập 365]
-
[Cho số phức z thỏa mãn (1+ 2i)2z + - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn: |z - (2 + i)| = - Luyện Tập 365]
-
[Tìm số phức z thỏa mãn |z-3i|=|1-i - Luyện Tập 365]
-
[Cho số phức zthỏa mãn (1 + i)2 (2 – i)z = 8 + i + (1 + - Luyện Tập 365]
-
[Giải phương trình sau trên tập hợp các số phức: - Luyện Tập 365]
-
[Gọi z1, z2 là hai nghiệm phức của phương trình z - Luyện Tập 365]
-
[Tìm số phức z, biết: z - (2 + 3i) - Luyện Tập 365]
-
[Cho số phức z thỏa mãn điều kiện (1 + i)(z – i) + 2z = 2i. Tính môđun củ - Luyện Tập 365]
-
[Cho số phức z = 1 + √3i. Viết dạng lượng giác của z. Tìm phần thực - Luyện Tập 365]
-
[Cho số phức z thỏa mãn điều kiện (3 + 2i)z + (2 – i)2 = 4 + i - Luyện Tập 365]
-
[Giải phương trình z2 + (2 – 3i)z – 1 – 3i = 0 trên tập hợp C - Luyện Tập 365]
-
[Giải phương trình 8z2 – 4z +1 = 0 trên tập số phức. - Luyện Tập 365]
.
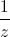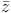= 4i – 20. Tính môđun của z.
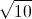và z.
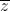= 25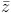
| và z-
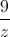là số thuần ảo
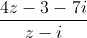= z - 2i
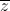= 1 - 9i
.
.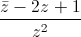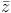