Trong mặt phẳng với hệ tọa độ Oxy, cho tam giácABC có A(1;1), trực tâm H(-1;3), tâm đường tròn ngoại tiếp I(3;-3). Xác định tọa độ các đỉnh B,C biết rằng xB<xC.
DANH SÁCH CÂU HỎI
-
[Trong mặt phẳng với hệ tọa độ Oxy, cho tam giácABC có A(1;1), trực tâm H - Luyện Tập 365]
-
[Cho hình chóp S, đáy ABCD là hình chữ nhật cạnh AB = a, AD = 2a hai mặt - Luyện Tập 365]
-
[Trong mặt phẳng tọa độ, giả sử điểm A biểu diễn nghiệmz1 - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục Oxy, cho hình chữ nhật ABCD. Hai điểm B và C - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho hai đường thẳng có phương trình: &nb - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục Oxy, cho hình chữ nhật ABCD có đường chéo AC - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục tọa độ Oxy cho∆ABC, với phương trình c - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục Oxy, cho hai điểm A(1 ; 0), B(3 ; 0). H là đ - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục Oxy, cho đường tròn (C): (x – 1)2 - Luyện Tập 365]
-
[Trong không gian với hệ tọa độ Oxyz, cho - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC có trọng tâm G(4 ; 3), - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục Oxy, cho đường thẳng∆: x - y = 0 và đư - Luyện Tập 365]
-
[Cho elip (E) có phương trình chính tắc: - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục Oxy, cho điểm E( 3; -1) và đường tròn ( C ): - Luyện Tập 365]
-
[Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC có đường cao AH: x + y - Luyện Tập 365]

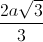 . Gọi K là giao điểm của SD với mặt phẳng (BCI). Tính thể tích khối chóp S.BCKI.
. Gọi K là giao điểm của SD với mặt phẳng (BCI). Tính thể tích khối chóp S.BCKI.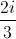 z1 . Chứng minh rằng tam giác OAB vuông
z1 . Chứng minh rằng tam giác OAB vuông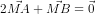
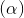 : 3x + 2y - z + 4 = 0, I(2; 2; 0). Tìm tọa độ điểm M biết rằng MI ⊥
: 3x + 2y - z + 4 = 0, I(2; 2; 0). Tìm tọa độ điểm M biết rằng MI ⊥ 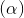 , đồng thời M cách đều gốc tọa độ và mặt phẳng
, đồng thời M cách đều gốc tọa độ và mặt phẳng 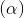
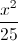 +
+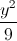 =1. Viết phương trình đường thẳng song song với Oy cắt (E) tại hai điểm A, B sao cho AB=4
=1. Viết phương trình đường thẳng song song với Oy cắt (E) tại hai điểm A, B sao cho AB=4