Cho điểm M(0;2) và hypebol (H):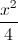 
-
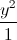=1.Lấp phương trình đường thẳng (d) đi qua điểm M cắt (H) tại hai điểm phân biệt A,B sao cho 
=
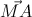DANH SÁCH CÂU HỎI
-
[Cho điểm M(0;2) và hypebol (H): - Luyện Tập 365]
-
[Cho hai điểm A(3; 2) và B(4; 0). Viết phương trình đường thẳng d đ - Luyện Tập 365]
-
[Cho tam giác ABC cân nội tiếp đường tròn tâm J bán kính R = 2a (a > 0 - Luyện Tập 365]
-
[Cho đường tròn (C) có bán kính R = 1, tiếp xúc với đường thẳng (d). Tính - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho 3 đường thẳng d1:x+y-2=0, d2 - Luyện Tập 365]
-
[Trong mặt phẳng (P) cho đường tròn ( C ) tâm O, đường kính AB = 2R; M là - Luyện Tập 365]
-
[Trong mặt phẳng Oxy, cho điểm A(2; 10) và đường thẳng d: y = 8. Điểm E d - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho đường thẳng d: y – 3 = 0 và A(1;1). Tìm điểm C t - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho đường tròn (C): x2 + y2 + - Luyện Tập 365]
-
[Trong mặt pẳng với hệ trục Oxy cho đường tròn: ( C1 ): x - Luyện Tập 365]
-
[Cho hai đường thẳng: d1: x + y – 2 = 0; d2 : 2x – - Luyện Tập 365]
-
[Cho họ đường tròn ( Cm) có phương trình: x2 + y - Luyện Tập 365]
-
[Trên các cạnh AB; BC; CD; DA có hình vuông ABCD lần lượt lấy 1, 2, 3, n - Luyện Tập 365]
-
[Trong mặt phẳng Oxy cho điểm I ( -2; 0 ) và hai đương thẳng: d1 - Luyện Tập 365]
-
[Cho lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a, khoảng cách từ - Luyện Tập 365]
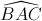= 120°. Trên đường thẳng vuông góc với mặt phẳng (ABC) lấy điểm S sao cho SA = a√3. Gọi I là trung điểm BC. Tính góc giữa SI và hình chiếu của nó trên mặt phẳng (ABC) và tính bán kính mặt cầu ngoại tiếp tứ dieejnSABC theo a.
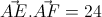. Điểm F chạy trên đường cong nào? Viết phương trình đường cong đó.
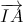= 2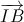
.
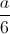. Tính thể tích của hình lăng trụ ABC.A’B’C’ theo a.