Luyện Thi Đại Học Môn Toán
Hệ Thức Lượng Trong Tam Giác Vuông
-
Cho tam giác vuông ABC (
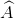 = 900), AB = 7,5 cm, AC = 10 cm, trung tuyến AM. Tính các tỉ số lượng giác của
= 900), AB = 7,5 cm, AC = 10 cm, trung tuyến AM. Tính các tỉ số lượng giác của 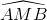 .
. -
Cho tam giác vuông cân ABC (
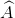 = 900, AB = AC). Trên cạn AC lấy điểm M sao cho MC : MA = 1 : 3. Kẻ đường thẳng vuông góc với AC tại C, cắt tia BM tại K. Kẻ BE ⊥ CK.
= 900, AB = AC). Trên cạn AC lấy điểm M sao cho MC : MA = 1 : 3. Kẻ đường thẳng vuông góc với AC tại C, cắt tia BM tại K. Kẻ BE ⊥ CK.a. Chứng minh tứ giác ABEC là hình vuông.
b. Chứng minh
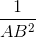 =
= 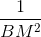 +
+ 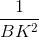
c. Biết BM = 6 cm. Tính các cạnh của tam giác MCK.
Hình Giải Tích Phẳng
-
Trong mặt phẳng Oxy cho ∆: x – 2y + 5 = 0. Viết phương trình (C) biết (C) tiếp xúc với ∆ tại điểm A(1; 3) và cắt Ox tại B, C sao cho ∆ABC có diện tích bằng 6.
-
Trong mặt phẳng xOy cho điểm M(2; 1) và đường thẳng d: x – y + 1 = 0. Viết phương trình đường tròn (C) đi qua M cắt d tại 2 điểm phân biệt sao cho ∆MAB vuông tại M và có diện tích bằng 2.
-
Trong mặt phẳng Oxy cho ∆ABC có đỉnh C(4; 3) đường phân giác trong và đường trung tuyến kẻ từ đỉnh A lần lượt có phương trình x + 2y – 5 = 0 và 4x + 13y – 10 = 0. Viết phương trình đường thẳng BC?
Hình Giải Tích Trong Không Gian
-
Trong không gian Oxyz, cho ba điểm A(2;1;-1), B(1;3;1), C(1;2;0). Viết phương trình đường thẳng (d) qua A, vuông góc và cắt đường thẳng BC.
-
Cho đường thẳng d:
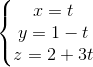 ; (P) x + y + z - 1 = 0
; (P) x + y + z - 1 = 0Viết phương trình mặt cầu (S) có tâm thuộc đường thẳng d tiếp xúc với (P) và có bán kính
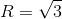
-
Cho hình hộp ABCDA'B'C'D' với A(1,1,1), B(3,2,1), D(1,2,1), B'(-1,0,2). Tìm tọa độ C', D' ?
Tổ Hợp - Xác Suất
-
Gọi X là tập hợp các số tự nhiên gồm năm chữ số đôi một khác nhau được tạo thành từ các chữ số 1,2,3,4,5,6,7,8,9. Chọn ngẫu nhiên mật số từ tập hợp X . Tính xác suất để số được chọn có tổng các chữ số là một số lẻ.
-
Một hộp đựng 3 bi xanh , 4 bi đỏ và 5 bi vàng . Lấy ngẫu nhiên 5 bi từ hộp . Tính xác suất để trong 5 bi lấy ra có đủ 3 màu và số bi xanh và số bi đỏ bằng nhau .
-
Gọi S là tập hợp các số gồm 5 chữ số khác nhau 0,1,2,3,4,5,6,7. Lấy ngẫu nhiên 1 số tự nhiên 1 số từ tập S. Tính xác suất để số lấy ra chỉ có mặt các chữ số lớn hơn 1 nhỏ hơn 7

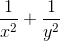 )
)


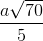 , đáy ABC là tam giác vuông tại A, AB = 2a , AC= a và hình chiếu của S lên mặt phẳng (ABC) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng BC và SA.
, đáy ABC là tam giác vuông tại A, AB = 2a , AC= a và hình chiếu của S lên mặt phẳng (ABC) là trung điểm của cạnh AB. Tính theo a thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng BC và SA.
![\int (3x^{2}-2).\sqrt[5]{(x-1)^{2}}dx](https://luyentap365.com/wp-content/picture/learning/exam/2014/1219/74366_987255_1.gif)