Bây giờ cho điểm A di động trên cung lớn BC của đường tròn (O; R). Chứng minh rằng bán kính đường tròn ngoại tiếp tam giác AED không đổi.
Câu hỏi
Nhận biếtBây giờ cho điểm A di động trên cung lớn BC của đường tròn (O; R). Chứng minh rằng bán kính đường tròn ngoại tiếp tam giác AED không đổi.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Vì KB = KC nên OK ┴ BC. Gọi giao điểm của BD với CE là H, ta có H là trực tâm của tam giác ABC, do đó AH ┴ BC.
Suy ra AH//OK (cùng ┴ BC)
Mặt khác,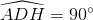 
nên AH là đường kính, do đó OA // O'K. Vì O'K là đường nối tâm, ED là dây cung nên O'K ┴ ED suy ra O'K // OA (vì cùng ┴ ED)
Vậy AO'KO là hình bình hành (vì O'A // OK; O'K // OA) và O'A = OK không đổi. Vậy bán kính đường tròn ngoại tiếp tam giác ADE không đổi.
Vì KB = KC nên OK ┴ BC. Gọi giao điểm của BD với CE là H, ta có H là trực tâm của tam giác ABC, do đó AH ┴ BC.
Suy ra AH//OK (cùng ┴ BC)
Mặt khác, 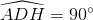nên AH là đường kính, do đó OA // O'K. Vì O'K là đường nối tâm, ED là dây cung nên O'K ┴ ED suy ra O'K // OA (vì cùng ┴ ED)
Vậy AO'KO là hình bình hành (vì O'A // OK; O'K // OA) và O'A = OK không đổi. Vậy bán kính đường tròn ngoại tiếp tam giác ADE không đổi.
Câu hỏi liên quan
-
Gọi hoành độ giao điểm 2 điểm M và N lần lượt là x1 và x2. Chứng minh rằng: x1x2=-1, từ đó suy ra tam giác MON là tam giác vuông
-
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Chứng minh DM.CE=DE.CM
-
Tìm a để phương trình có 2 nghiệm nguyên
-
Cho biểu thức A = (
- 
+ 
) : ( x - 2 + 
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-
Giải hệ phương trình
-
Cho biểu thức:
A =
Trả lời câu hỏi dưới đây:
Rút gọn A
-
Rút gọn biểu thức A
-
Tìm b để A =
