a. Phát biểu quy tắc khai phương một tích (HS tự làm)
b. Áp dung: Hãy tính
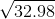 ,
, 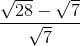

Câu hỏi
Nhận biếta. Phát biểu quy tắc khai phương một tích (HS tự làm)
b. Áp dung: Hãy tính
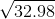 ,
, 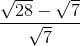
A.
Xem phần lời giải
Đáp án đúng: A
Lời giải của Luyện Tập 365
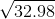 =
= 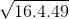 =
= 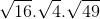 = 4.2.7 = 56
= 4.2.7 = 56
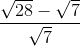 =
= 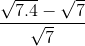 =
= 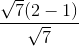 = 1
= 1
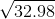 =
= 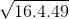 =
= 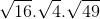 = 4.2.7 = 56
= 4.2.7 = 56
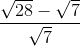 =
= 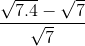 =
= 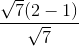 = 1
= 1
Câu hỏi liên quan
-

Tìm b để A =

-

Tìm a để phương trình có 2 nghiệm nguyên
-

Chứng minh DM.CE=DE.CM
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Rút gọn biểu thức A
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Chứng minh rằng: AM2 = AN.AB
-

Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Tính giá trị biểu thức của A với x =

-

Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
