Điện năng từ một nhà máy đc đưa đến nơi tiêu thu nhờ các dây dẫn, tại nơi tiêu thụ cần một công suất không đổi. Banđầu hiệu suất tải điện là 90%. Muốn hiệu suất tải điện là 96% cần giảm cường độ dòng điện trên dây tải đi

Câu hỏi
Nhận biếtĐiện năng từ một nhà máy đc đưa đến nơi tiêu thu nhờ các dây dẫn, tại nơi tiêu thụ cần một công suất không đổi. Banđầu hiệu suất tải điện là 90%. Muốn hiệu suất tải điện là 96% cần giảm cường độ dòng điện trên dây tải đi
Đáp án đúng: D
Phương pháp giải
Ta có công thức tính công suất hao phí: \(P = {I^2}R\)
Công thức xác định hiệu suất:
\(\eqalign{
& H = {{{P_{tt}}} \over {{P_{tp}}}} = {{P - {P_{hp}}} \over P} \Rightarrow P = {{{P_{hp}}} \over {1 - H}} \cr
& \Rightarrow \left\{ \matrix{
{P_1} = {{{P_{hp1}}} \over {1 - {H_1}}} \hfill \cr
{P_2} = {{{P_{hp2}}} \over {1 - {H_2}}} \hfill \cr} \right. \cr} \)
Ta có công thức tính công suất hao phí: \(P = {I^2}R\)
Công thức xác định hiệu suất:
\(\eqalign{
& H = {{{P_{tt}}} \over {{P_{tp}}}} = {{P - {P_{hp}}} \over P} \Rightarrow P = {{{P_{hp}}} \over {1 - H}} \cr
& \Rightarrow \left\{ \matrix{
{P_1} = {{{P_{hp1}}} \over {1 - {H_1}}} \hfill \cr
{P_2} = {{{P_{hp2}}} \over {1 - {H_2}}} \hfill \cr} \right. \cr} \)
Lời giải của Luyện Tập 365
Ta có công thức tính công suất hao phí: \(P = {I^2}R\)
Công thức xác định hiệu suất:
\(\eqalign{
& H = {{{P_{tt}}} \over {{P_{tp}}}} = {{P - {P_{hp}}} \over P} \Rightarrow P = {{{P_{hp}}} \over {1 - H}} \cr
& \Rightarrow \left\{ \matrix{
{P_1} = {{{P_{hp1}}} \over {1 - {H_1}}} \hfill \cr
{P_2} = {{{P_{hp2}}} \over {1 - {H_2}}} \hfill \cr} \right. \cr} \)
Vì công suất tại nơi tiêu thụ không đổi nên:
\(\eqalign{
& {P_1}{H_1} = {P_2}{H_2} \Leftrightarrow {{{P_{hp1}}.{H_1}} \over {1 - {H_1}}} = {{{P_{hp2}}.{H_2}} \over {1 - {H_2}}} \cr
& \Leftrightarrow {{{P_{hp1}}} \over {\left( {1 - {H_1}} \right){H_2}}} = {{{P_{hp2}}} \over {\left( {1 - {H_2}} \right){H_1}}} \Leftrightarrow {{{P_{hp1}}} \over {{P_{hp2}}}} = {{\left( {1 - {H_1}} \right){H_2}} \over {\left( {1 - {H_2}} \right){H_1}}} \cr
& \Leftrightarrow {{I_1^2} \over {I_2^2}} = {{\left( {1 - {H_1}} \right){H_2}} \over {\left( {1 - {H_2}} \right){H_1}}} \Rightarrow {{{I_2}} \over {{I_1}}} = \sqrt {{{\left( {1 - {H_2}} \right){H_1}} \over {\left( {1 - {H_1}} \right){H_2}}}} \cr
& \Rightarrow {{{I_2}} \over {{I_1}}} = \sqrt {{{\left( {1 - 0,96} \right).0,9} \over {\left( {1 - 0,9} \right).0,96}}} = 0,6124 \cr
& \Rightarrow {I_2} = 0,6124.{I_1} \cr
& \Rightarrow {{\Delta I} \over {{I_1}}} = {{{I_1} - {I_2}} \over {{I_1}}} = {{{I_1} - 0,6124{I_1}} \over {{I_1}}} = 38,76\% \cr} \)
Ta có công thức tính công suất hao phí: \(P = {I^2}R\)
Công thức xác định hiệu suất:
\(\eqalign{
& H = {{{P_{tt}}} \over {{P_{tp}}}} = {{P - {P_{hp}}} \over P} \Rightarrow P = {{{P_{hp}}} \over {1 - H}} \cr
& \Rightarrow \left\{ \matrix{
{P_1} = {{{P_{hp1}}} \over {1 - {H_1}}} \hfill \cr
{P_2} = {{{P_{hp2}}} \over {1 - {H_2}}} \hfill \cr} \right. \cr} \)
Vì công suất tại nơi tiêu thụ không đổi nên:
\(\eqalign{
& {P_1}{H_1} = {P_2}{H_2} \Leftrightarrow {{{P_{hp1}}.{H_1}} \over {1 - {H_1}}} = {{{P_{hp2}}.{H_2}} \over {1 - {H_2}}} \cr
& \Leftrightarrow {{{P_{hp1}}} \over {\left( {1 - {H_1}} \right){H_2}}} = {{{P_{hp2}}} \over {\left( {1 - {H_2}} \right){H_1}}} \Leftrightarrow {{{P_{hp1}}} \over {{P_{hp2}}}} = {{\left( {1 - {H_1}} \right){H_2}} \over {\left( {1 - {H_2}} \right){H_1}}} \cr
& \Leftrightarrow {{I_1^2} \over {I_2^2}} = {{\left( {1 - {H_1}} \right){H_2}} \over {\left( {1 - {H_2}} \right){H_1}}} \Rightarrow {{{I_2}} \over {{I_1}}} = \sqrt {{{\left( {1 - {H_2}} \right){H_1}} \over {\left( {1 - {H_1}} \right){H_2}}}} \cr
& \Rightarrow {{{I_2}} \over {{I_1}}} = \sqrt {{{\left( {1 - 0,96} \right).0,9} \over {\left( {1 - 0,9} \right).0,96}}} = 0,6124 \cr
& \Rightarrow {I_2} = 0,6124.{I_1} \cr
& \Rightarrow {{\Delta I} \over {{I_1}}} = {{{I_1} - {I_2}} \over {{I_1}}} = {{{I_1} - 0,6124{I_1}} \over {{I_1}}} = 38,76\% \cr} \)
Câu hỏi liên quan
-

Phát biểu nào sau đây là không đúng? Gia tốc của một vật dao động điều hòa
-

Tại sao khi chùm tia sáng mặt trời đi qua một tấm thủy tinh phẳng lại không thấy bị tán sắc thành những màu cơ bản?
-

Một vật nhỏ dao động điều hòa theo một trục cố định. Phát biểu nào sau đây đúng?
-

Ánh sáng có tần số lớn nhất trong số các ánh sáng đơn sắc: đỏ, lam, chàm, tím là ánh sáng:
-

Khi chiếu ánh sáng trắng vào một lăng kính thì tia sáng nào bị lệch về phía đáy nhiều nhất ?
-

Trong chương trình của vật dao động điều hòa x = Acos(ωt + φ), radian trên giây (rad/s) là đơn vị của đại lượng nào sau đây:
-

Phát biểu nào dưới đây là sai khi nói về ánh sáng trắng và ánh sáng đơn sắc:
-

Câu nào dưới đây không đúng với vật dao động điều hòa có phương trình x = Acos(
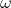 t +
t + 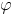 )
) -

Câu phát biểu nào sau đây về hiện tượng tán sắc là sai ?
-

Chuyển động nào sau đây của chất điểm là một dao động điều hòa?
