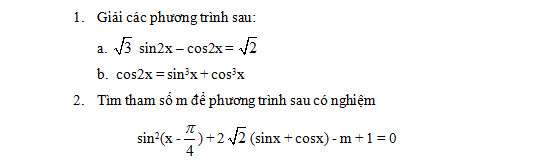Cho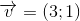 
và đường thẳng d: y=2x+4. Tìm ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 
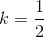và phép tịnh tiến theo vecto 
.
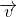Câu hỏi
Nhận biếtCho 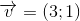và đường thẳng d: y=2x+4. Tìm ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 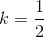và phép tịnh tiến theo vecto .
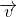Đáp án đúng:
Lời giải của Luyện Tập 365
Lấy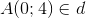 
=>
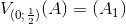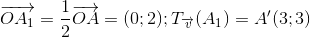
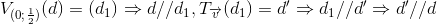
Phương trình d' có dạng : y=2x+b
Do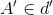 
nên : 3=6+b <=> b=-3
Phương trình đường thẳng (d'): y=2x-3
Lấy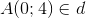
=>
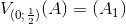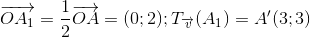
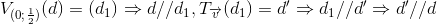
Phương trình d' có dạng : y=2x+b
Do 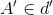nên : 3=6+b <=> b=-3
Phương trình đường thẳng (d'): y=2x-3
Câu hỏi liên quan
-
-
-
Có bao nhiêu cách sắp xếp 5 bạn học sinh A, B, C, D, E ngồi vào một chiếc ghế dài sao cho:
a. Bạn C ngồi chính giữa?
b. Hai bạn A và E ngồi ở hai đầu ghế?
-
Gieo một con súc sắc cân đối đồng chất hai lần. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 8.
b) Tích số chấm hai mặt xuất hiện là số lẻ.
-
-
-
Cho
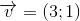và đường thẳng d: y=2x+2 Tìm ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 
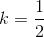và phép tịnh tiến theo vectơ . -
Gieo hai con súc sắc cân đối đồng chất. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 7.
b) Các mặt xuất hiện có số chấm bằng nhau.
-
bai 3 de 2 HK1 minh khai ha tinh 13-14
-
