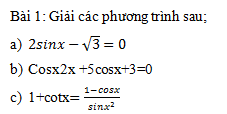Gieo hai con súc sắc cân đối đồng chất. Tính xác suất của biến cố: a) Tổng số chấm hai mặt xuất hiện bằng 7. b) Các mặt xuất hiện có số chấm bằng nhau.
Câu hỏi
Nhận biếtGieo hai con súc sắc cân đối đồng chất. Tính xác suất của biến cố:
a) Tổng số chấm hai mặt xuất hiện bằng 7.
b) Các mặt xuất hiện có số chấm bằng nhau.
Đáp án đúng:
Lời giải của Luyện Tập 365
a)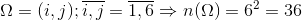 
Gọi A: “Tổng số chấm hai mặt xuất hiện bằng 7"
A={(1;6),(2;5);(3;4),(4;3),(5;2),(6;1)} =>n(A)=6
=>P(A)=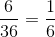
b)
Gọi B là biến cố: “ Các mặt xuất hiện có số chấm bằng nhau ”
B={(1;1),(2;2),(3;3),(4;4),(5;5),(6,6)} =>n(B)=6
=>P(B)=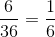
a)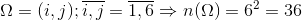
Gọi A: “Tổng số chấm hai mặt xuất hiện bằng 7"
A={(1;6),(2;5);(3;4),(4;3),(5;2),(6;1)} =>n(A)=6
=>P(A)=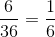
b)
Gọi B là biến cố: “ Các mặt xuất hiện có số chấm bằng nhau ”
B={(1;1),(2;2),(3;3),(4;4),(5;5),(6,6)} =>n(B)=6
=>P(B)=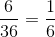
Câu hỏi liên quan
-
Giải các phương trình sau:
a)
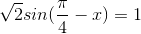
b)
-
-
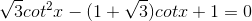
Cho 5 điểm phân biệt trong mặt phẳng và không có 3 điểm nào thẳng hàng. Hỏi:
a. Có bao nhiêu vectơ tạo thành từ 5 điểm ấy?
b. Có bao nhiêu đoạn thẳng tạo thành từ 5 điểm ấy?
-
Tìm tập xác định của các hàm số sau:
-
-
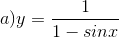
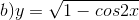
Tìm số hạng không chứa x trong khai triển của nhị thức
-
-
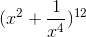
Cho
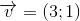và đường thẳng d: y=2x+2 Tìm ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số 
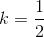và phép tịnh tiến theo vectơ . -
-
: Cho hình chóp S.ABCD có đáy ABCD là hình thang (AD là đáy lớn).
a) Xác định giao tuyến của hai cặp mặt phẳng (SAC) và (SBD) ;(SAD) và (SBC).
b) M là một điểm trên cạnh SC không trùng với S và C. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (ABM).
c) Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC), chứng minh d và BM đồng phẳng.
