Hãy tính: 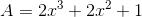 với
với ![x=\frac{1}{3}(\sqrt[3]{\frac{23+\sqrt{513}}{4}}+\sqrt[3]{\frac{23-\sqrt{513}}{4}}-1)](https://luyentap365.com/wp-content/picture/learning/exam/2014/0508/56698_603623_2.gif)

Câu hỏi
Nhận biếtHãy tính: 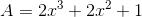 với
với ![x=\frac{1}{3}(\sqrt[3]{\frac{23+\sqrt{513}}{4}}+\sqrt[3]{\frac{23-\sqrt{513}}{4}}-1)](https://luyentap365.com/wp-content/picture/learning/exam/2014/0508/56698_603623_2.gif)
A.
A = 0
B.
A = 1
C.
A = 2
D.
A= 3
Đáp án đúng: C
Lời giải của Luyện Tập 365
Đặt: ![a=\sqrt[3]{\frac{23+\sqrt{513}}{4}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0508/v51779_303906_1.gif) ;
; ![b=\sqrt[3]{\frac{23-\sqrt{513}}{4}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0508/v51779_530657_2.gif) ; y = a + b
; y = a + b
Ta có: 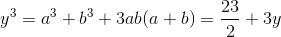
Ta có: 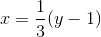 <=> y = 3x + 1.
<=> y = 3x + 1.
Thay vào biểu thức trên ta tính được A = 2
Đặt: ![a=\sqrt[3]{\frac{23+\sqrt{513}}{4}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0508/v51779_303906_1.gif) ;
; ![b=\sqrt[3]{\frac{23-\sqrt{513}}{4}}](https://luyentap365.com/wp-content/picture/learning/exam/2014/0508/v51779_530657_2.gif) ; y = a + b
; y = a + b
Ta có: 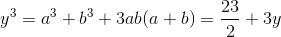
Ta có: 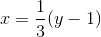 <=> y = 3x + 1.
<=> y = 3x + 1.
Thay vào biểu thức trên ta tính được A = 2
Câu hỏi liên quan
-

Rút gọn biểu thức A
-

Tính AC và BD biết
 =
=  . Chứng tỏ tích AC.BD không phụ thuộc vào
. Chứng tỏ tích AC.BD không phụ thuộc vào 
-

Tìm m để phương trình (1) có nghiệm .
-

Rút gọn A
-

Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Tính giá trị biểu thức của A với x =

-

Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-

Giải phương trình với a = -2
-

Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
