Cho tam giác cân ABC, đáy BC = 6 cm, chiều cao AH = 4 cm, nội tiếp đường tròn (O). Trả lời câu hỏi dưới đây:Vẽ AK ┴ BB'. Chứng minh AK = AM và tứ giác BHKA là hình thang cân
Câu hỏi
Nhận biếtCho tam giác cân ABC, đáy BC = 6 cm, chiều cao AH = 4 cm, nội tiếp đường tròn (O).
Trả lời câu hỏi dưới đây:
Vẽ AK ┴ BB'. Chứng minh AK = AM và tứ giác BHKA là hình thang cân
Đáp án đúng: A
Lời giải của Luyện Tập 365
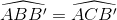(hai góc nội tiếp cùng chắn cung AB'). Hai tam giác vuông AKB và AMC bằng nhau vì có cạnh huyền và góc nhọn bằng nhau, do đó AK = AM.
Tứ giác BHKA nội tiếp được một đường tròn vì có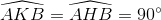 
Trong đường tròn này ta lại có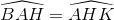 
(vì cùng bằng góc ABK) nên AB // HK. Hình thang ABHK nội tiếp đường tròn nên là hình thang cân
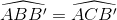(hai góc nội tiếp cùng chắn cung AB'). Hai tam giác vuông AKB và AMC bằng nhau vì có cạnh huyền và góc nhọn bằng nhau, do đó AK = AM.
Tứ giác BHKA nội tiếp được một đường tròn vì có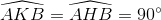
Trong đường tròn này ta lại có 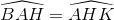(vì cùng bằng góc ABK) nên AB // HK. Hình thang ABHK nội tiếp đường tròn nên là hình thang cân
Câu hỏi liên quan
-
Giải phương trình với a = -2
-
Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-
Tìm a để phương trình có 2 nghiệm nguyên
-
Tính giá trị biểu thức của A với x =
-
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Tìm m để phương trình (1) có nghiệm .
-
Gọ M là tiếp điểm của tiếp tuyến kẻ từ E với nửa đường tròn (O). Chứng minh tứ giác ACMO nội tiếp.
-
Giải phương trình (1) khi m = -5
-
Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB