Từ điểm P cố định nằm ngoài đường tròn (O; R) cho trước vẽ tiếp tuyến PA và cát tuyến PBC. Gọi H là trực tâm của tam giác ABC, H1 là điể đối xứng của H qua BC, O1 là điểm đối xứng của O qua BC. Trả lời câu hỏi dưới đây:Chứng minh H1 nằm trên đường tròn (O)
Câu hỏi
Nhận biếtTừ điểm P cố định nằm ngoài đường tròn (O; R) cho trước vẽ tiếp tuyến PA và cát tuyến PBC. Gọi H là trực tâm của tam giác ABC, H1 là điể đối xứng của H qua BC, O1 là điểm đối xứng của O qua BC.
Trả lời câu hỏi dưới đây:
Chứng minh H1 nằm trên đường tròn (O)
Đáp án đúng: A
Lời giải của Luyện Tập 365
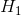đối xứng với H qua BC nên 
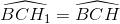mà 
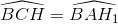(góc có cạnh tương ứng vuông góc) suy ra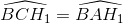 
Tứ giác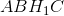 
nội tiếp đường tròn
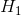=> ϵ (O)
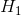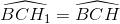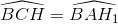đối xứng với H qua BC nên mà (góc có cạnh tương ứng vuông góc) suy ra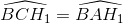
Tứ giác 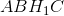nội tiếp đường tròn
=> ϵ (O)
Câu hỏi liên quan
-
AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-
Giải phương trình (1) khi m = -5
-
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Giải hệ phương trình với a = 2
-
Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-
Rút gọn A
-
Tìm a để hệ phương trình có một nghiệm số duy nhất thỏa mãn: x2 - 12x – 14y < 0
-
Giải phương trình với a = -2
-
Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
-
Tìm m để phương trình (1) có nghiệm .