Cho hai đường tròn (O); (O') cắt nhau tại hai điểm A, B. Các đường thẳng AO, AO' cắt đường tròn (O) lần lượt tại các điểm thứ hai C, D và cắt đường tròn (O') lần lượt tại các điểm thứ hai E, F. Trả lời câu hỏi dưới đây:Chứng minh rằng A là tâm đường tròn nội tiếp tam giác BDE.
Câu hỏi
Nhận biếtCho hai đường tròn (O); (O') cắt nhau tại hai điểm A, B. Các đường thẳng AO, AO' cắt đường tròn (O) lần lượt tại các điểm thứ hai C, D và cắt đường tròn (O') lần lượt tại các điểm thứ hai E, F.
Trả lời câu hỏi dưới đây:
Chứng minh rằng A là tâm đường tròn nội tiếp tam giác BDE.
Đáp án đúng: A
Lời giải của Luyện Tập 365
Do các tứ giác CDEF, BAEF nội tiếp được nên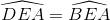 
(vì cùng bằng 
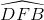). Vậy tia EA là phân giác của góc DEB. Tương tự, tia DA là tia phân giác của góc EDB. Suy ra A là tâm đường tròn nội tiếp tam giác BDE.
Do các tứ giác CDEF, BAEF nội tiếp được nên 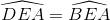(vì cùng bằng 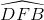). Vậy tia EA là phân giác của góc DEB. Tương tự, tia DA là tia phân giác của góc EDB. Suy ra A là tâm đường tròn nội tiếp tam giác BDE.
Câu hỏi liên quan
-
Cho nửa đường tròn tâm O đường kính MN. Từ một điểm A trên tiếp tuyến Mx của nửa đường tròn (O), vẽ tiếp tuyến thứ hai AE ( E là tiếp điểm). Nối A với N cắt nủa đưởng tròn (O) ở B.
Trả lời câu hỏi dưới đây:
Chứng minh rằng: AM2 = AN.AB
-
Giải hệ phương trình với a = 2
-
Chứng minh rằng d luôn cắt (P) tại 2 điểm phân biệt M và N với mọi K
-
Cho Parabol (P): ax2(a ≠ 0) và đường thẳng d: y=2x - a. Tìm điểm a để d tiếp xúc với (P). Tìm tọa độ tiếp điểm.
-
Cho biểu thức A = (
- 
+ 
) : ( x - 2 + 
)Trả lời câu hỏi dưới đây:
Rút gọn biểu thức A
-
Giải phương trình (1) khi m = -5
-
Giải phương trình với a = -2
-
Trong mặt phẳng tọa độ Oxy cho Parabol (P): y=x2và điểm A(0;1)
Trả lời câu hỏi dưới đây:
Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-
Cho biểu thức:
A =
Trả lời câu hỏi dưới đây:
Rút gọn A
-
Rút gọn biểu thức A