Một tam giác đều ABC nội tiếp đường tròn (O) đường kính AD = 6,0 cm. Gọi I là giao điểm của hai đường thẳng BD và AC. Trên tia IC lấy điểm N sao cho IN = IB; đường thẳng BN cắt đường tròn tại điểm thứ hai M. Trả lời câu hỏi dưới đây:Các tam giác BIN và BMD là tam giác gì?

Câu hỏi
Nhận biếtMột tam giác đều ABC nội tiếp đường tròn (O) đường kính AD = 6,0 cm. Gọi I là giao điểm của hai đường thẳng BD và AC. Trên tia IC lấy điểm N sao cho IN = IB; đường thẳng BN cắt đường tròn tại điểm thứ hai M.
Trả lời câu hỏi dưới đây:
Các tam giác BIN và BMD là tam giác gì?
Đáp án đúng: B
Lời giải của Luyện Tập 365
IB = IN (gt) => ∆ BIN cân
Dễ dàng chứng minh được 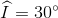
=> 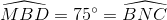
=> 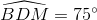 => ∆ BMD cân
=> ∆ BMD cân
IB = IN (gt) => ∆ BIN cân
Dễ dàng chứng minh được 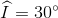
=> 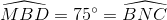
=> 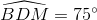 => ∆ BMD cân
=> ∆ BMD cân
Câu hỏi liên quan
-

Cho phương trình x2- 4x + m = 0 (1), với m là tham số.
Trả lời câu hỏi dưới đây:
Giải phương trình (1) khi m = -5
-

Chứng minh DM.CE=DE.CM
-

Chứng minh rằng: AM2 = AN.AB
-

Rút gọn biểu thức A
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Tính AC và BD biết
 =
=  . Chứng tỏ tích AC.BD không phụ thuộc vào
. Chứng tỏ tích AC.BD không phụ thuộc vào 
-

Rút gọn A
-

Tìm b để A =

-

Tìm đường thẳng d biết đường thẳng đó đi qua A(0;1) và có hệ số góc k
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
