Hai đường tròn (O; 3,0cm) và (O'; 9,0 cm) tiếp xúc ngoài với nhau. Tính diện tích hình giới hạn bởi hai đường tròn và hai tiếp tuyến chung ngoài của chúng.


Câu hỏi
Nhận biếtHai đường tròn (O; 3,0cm) và (O'; 9,0 cm) tiếp xúc ngoài với nhau. Tính diện tích hình giới hạn bởi hai đường tròn và hai tiếp tuyến chung ngoài của chúng.

Đáp án đúng: C
Lời giải của Luyện Tập 365
Gọi S là diện tích tam giác cong ABC thì diện tích phải tìm là 2S (phần gạch sọc). Ta có S bằng diện tích hình thang ABOO' trừ đi tổng diện tích hai hình quạt OCB và O'CA. Ta có: AB2 = OH2 = OO’2 – O’H2 = (OO’ + O’H)(OO’ – O’H).
(9,0 + 3,0)(9,0 - 3,0) = 72 hay 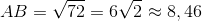
Ta lại có 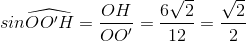
hay 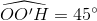 và
và 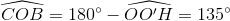 . Do đó:
. Do đó:
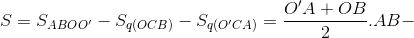
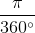 .135.
.135.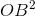
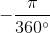 .
.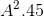
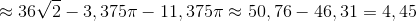
và 2S = 2. 4,45 = 8,9 cm2.
Gọi S là diện tích tam giác cong ABC thì diện tích phải tìm là 2S (phần gạch sọc). Ta có S bằng diện tích hình thang ABOO' trừ đi tổng diện tích hai hình quạt OCB và O'CA. Ta có: AB2 = OH2 = OO’2 – O’H2 = (OO’ + O’H)(OO’ – O’H).
(9,0 + 3,0)(9,0 - 3,0) = 72 hay 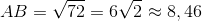
Ta lại có 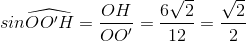
hay 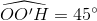 và
và 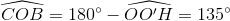 . Do đó:
. Do đó:
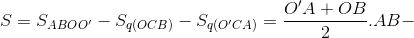
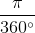 .135.
.135.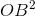
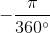 .
.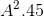
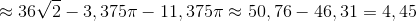
và 2S = 2. 4,45 = 8,9 cm2.
Câu hỏi liên quan
-

Giải hệ phương trình

-

AO cắt ME tại C. Chứng minh tứ giác ABCM nội tiếp.
-

Cho biểu thức:
A =

Trả lời câu hỏi dưới đây:
Rút gọn A
-

Cho hệ phương trình:

Trả lời câu hỏi dưới đây:
Giải hệ phương trình với a = 2
-

Rút gọn A
-

Tìm b để A =

-

Giải phương trình với a = -2
-

Chứng minh rằng phương trình (1) luôn có nghiệm với mọi a
-

Kẻ EI vuông góc MN, cắt AN tại D. Tính CD biết ME = 8cm; MN=10cm
-

Cho phương trình:
ax2 – 2(2a – 1) x+ 3a – 2 = 0 (1)
Trả lời câu hỏi dưới đây:
Giải phương trình với a = -2
